O modelo de predição linear

Introdução

Hoje assunto será o modelo de predição linear. Este modelo é bem antigo e vem sendo utilizado na estatística por mais de 50 anos. Como o próprio nome sugere, o modelo linear parte do princípio que o seu problema pode ser aproximado linearmente, ou seja, se ele for um modelo 2D, ele deve ser aproximado por uma reta, como mostrado na Figura 1. Daí você pode estar se perguntando: mas a maioria dos problemas do mundo são não lineares. Pra que aprender isso? Bom, essa afirmação é verdadeira. Porém, o modelo linear pode ser aplicados em muitos problemas. As vezes, ele gera um erro tão próximo de um não linear, que pela sua simplicidade, vale a pena utilizá-lo. Além disso, esse modelo é uma excelente iniciação na área de machine learning , uma vez que podemos trabalhar conceitos importantes de maneira simples, pois o problema é mais simples.

Figura 1: Exemplo de uma aproximação linear para um dado problema. Fonte: [1]

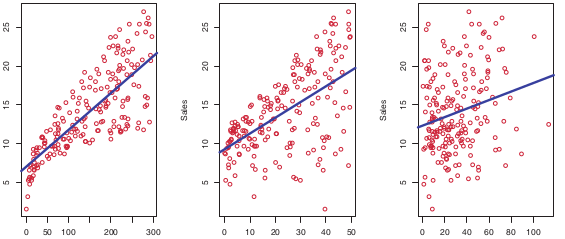
Nela vamos discutir a natureza matemática do problema e já apresentar a primeira solução para ele. Já aviso que será um post que vai misturar estatística, matemática e programação, ou seja, vamos discutir o modelo teórico e vamos implementá-lo em Python. Essa vai ser a pegada desse curso. Sem mais delongas, vamos iniciar!

O modelo linear

Vamos iniciar a descrição do nosso modelo linear com um pequeno exemplo. Imagine que você precisa desenvolver um modelo para estimar a idade de uma pessoa tendo como informação apenas a altura e o peso da mesma. Bom, provavelmente isso seja impossível, é necessário mais dados, mas vamos fingir que isso é o suficiente. Neste caso, temos uma variável \(X\) de duas dimensões assumindo os valores de altura (\(x_1\)) e peso (\(x_2\)). Por outro lado, temos uma variável de saída \(y\) que será o resultado, no caso a idade da pessoa. Vamos supor que já sabemos como resolver esse problema e para descobrir a idade temos que aplicar a seguinte função linear:

\[y(x_1, x_2) = 3.11 + 8.8x_1 + 0.1x_2 \tag{1}\]

Sendo assim, segundo nossa equação, uma pessoa com 90kg e 1.90m de altura, terá por volta de 28 anos (mais uma vez, isso é apenas uma ilustração).

\[y(1.9, 90) = 3.11 + 8.8 \times 1.9 + 0.1 \times 90 = 28.83 \tag{2}\]

O ponto aqui é que as variáveis chaves da nossa equação 2 são valores \(3.11, 8.8\) e \(0.1\). A pergunta que temos que fazer aqui é: como descobrir esses valores? Até porque são eles que vão regir o modelo. Para começar. precisamos generalizar o nosso problema. Primeiramente, podemos utilizar a seguinte generalização:

\[y(x_1, x_2) = a + bx_1 + cx_2 \tag{3}\]

Agora fica claro que desejamos encontrar os valores de \(a, b\) e \(c\). Porém, essa generalização não é suficiente. Ela assume que o problema será sempre de duas dimensões, ou seja, teremos sempre \(x_1\) e \(x_2\). Portanto, para uma geralização completa, asssumimos uma entrada \(\mathbf{x} = (x_1, x_2, \cdots, x_k)\), na qual \(k\) será a dimensão do problema, e uma saída \(\hat{y}\). Com isso, nosso problema, finalmente, será representado por:

\[\hat{y}(\mathbf{x}) = w_0 + \sum_{j=1}^k x_jw_j \tag{4}\]

Sendo que o objetivo aqui é determinar o valores de \(\mathbf{w} =\{w_0, \cdots, w_j\}\), nossos antigos parâmetros \(a, b\) e \(c\). A variável \(\hat{y}\) ganhou um “chapéu” pois ela representa um valor estimado, ou seja, é uma aproximação do mundo real, mas pode não ser a realidade. Se voltarmos ao nosso exemplo de estimar a idade da pessoa, segundo nossa equação 4, a variável \(X\) armazenaria dados de \(N\) pessoas com dimensão \(p\). Como uma pessoa, neste problema, é presentada por duas variáveis (altura e peso), se tivermos 10 pessoas, \(X\) seria uma matriz \(N \times k\), na qual cada linha contém uma pessoa. Por sua vez, \(\mathbf{y}\) seria um array com \(N\) idades, uma para cada pessoa da matriz \(X\).

Observe que o modelo linear possui um parâmetro independente (\(w_0\)) e \(k\) parâmetros dependentes, ou seja, ele são relacionados as \(k\) variáveis de entrada (\(\mathbf{x}\)) do modelo. Esse termo independente é conhecido como bias e você pode interpretá-lo como um valor padrão do modelo, ou seja, quando tudo for zero, só vai sobrar ele. Além disso, se imaginarmos uma reta, ele tem o poder de alterar a posição da mesma no eixo y (lembra das aulas do ensino médio? Da equação de reta \(f(x) = ax + b\)?).

Um truque matemático

Para facilitar a manipulação matemática e a implementação do modelo linear, é utilizado a notação matricial. Na verdade, sempre que possível, devemos programar os algoritmos dessa forma. Em inglês isso é chamado de vectorization. A grande vantagem, além de facilitar a notação, é que a execução do nosso código fica mais rápido. A maioria das bibliotecas de manipulação de matrizes/arrays são bem otimizadas nesse aspecto. Além disso, isso facilita o paralelismo. Todavia, ainda é possível melhorar a equação 4. Daí que vem o truque (ou trick, em inglês). Primeiro, vamos incorporar o bias dentro do array de pesos \(\mathbf{w}\) e obtermos a equação 4 da seguinte forma:

\[\hat{y}(\mathbf{x}) = \sum_{j=0}^k x_jw_j \tag{5}\]

Para isso, temos que anexar uma entrada unitária ao valor de \(\mathbf{x}\), que passará a ser \(\mathbf{x} = \{1, x_1, \cdots, x_k\}\). Agora faça os cálculos e perceba que o valor é o mesmo. Agora, vamos vetorizar de fato a equação. No post sobre álgebra linear falamos do produto escalar (ou dot product). Vamos usá-lo agora para vetorizar a equação 5:

\[\hat{y}(\mathbf{x}) = \mathbf{w}^{\top} \times \mathbf{x} \tag{6}\]

Computacionalmente falando, reduzimos o nosso modelo linear a uma multiplicação de arrays, na qual \(\mathbf{x} = [1, x_1, \cdots, x_k]\) e \(\mathbf{w} = [w_0, w_1, \cdots, w_k]\). No momento, usar a transposta de \(\mathbf{w}\) não faz muita diferença. Mas será útil mais para frente. Logo, já vamos começar com essa notação. Ótimo, mas a pergunta ainda persiste: como determinar os valores de \(\mathbf{w}\). Bom, precisamos treinar o nosso modelo!

Treinando um modelo linear

O treinamento de qualquer modelo de machine learning nada mais é que um processo de otimização na qual temos que descobrir os parâmetros do modelo. O primeiro passo para iniciar um algoritmo de treinamento (além de ter os dados, é claro) é determinar uma métrica de erro.

Função de erro

Para treinar um algoritmo de machine learning, precisamos de alguma métrica de qualidade. Temos que determinar uma função que determine um erro. Em inglês, essa função pode ser chamada de loss function. Normalmente, ela retorna um valor, maior que zero, que quanto menor melhor. Predições perfeitas do nosso modelo, retornariam erro zero. Predições ruins, retornariam erros muito alto (esse alto depende da entrada). Uma das funções mais comuns para problemas de regressão é o erro quadrático médio (ou mean square error) MSE, que definido da seguinte forma:

\[MSE(\mathbf{w}) = \frac{1}{2N} \sum_{i=0}^N(y_i - \hat{y}_i) \tag{7}\]

Na qual \(N\) é o numero de amostras, como já mencionamos anteriormente, \(\hat{y}\) é a predição do nosso modelo e \(y\) é o valor real da entrada. Dois pontos relevantes aqui: (1) essa é uma função quadrática, o que significa que ela sempre tem um mínimo, mas não necessáriamente esse mínimo é único; (2) O termos \(1/2\) não afeta no erro, ele é apenas mais um truque matemático que vai ser útil para o cálculo da derivada.

Graficamente, o intuito dessa equação é obter o erro de todas as estimações, como mostrado na Figura 1, e calcular a média de todos eles.

Figura 1: ilustração gráfica do calculo do erro. Fonte [2]

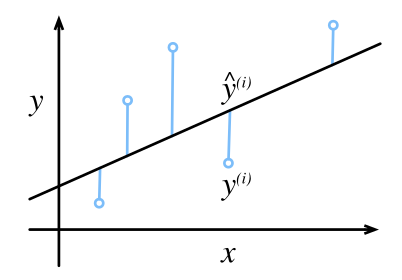
Podemos substituir \(\hat{y}\) na equação 7 utilizando a equação 6. Dessa forma, temos:

\[MSE(\mathbf{w}) = \frac{1}{2N} \sum_{i=0}^N(y_i - \mathbf{w}^{\top} \times \mathbf{x}_i) \tag{8}\]

Portanto, agora que temos a função de erro, devemos propor um algoritmo de otimização que seja capaz de minimizar esse erro dado os parâmetros, nese caso, \(\mathbf{w}\). Se você acompanha este blog, já deve saber que existem diversos algoritmos de otimização. Se você não sabe nada sobre o assunto, de uma olhada no post sobre o problema de otimização. Neste post, vamos apresentar dois métodos para treinar o modelo linear. Um analítico e outro iterativo.

Método dos mínimos quadrados

O método dos mínimos quadrados é um método analítico que visa encontrar \(\mathbf{w}\) tal que a derivada do erro seja zero. Lembre-se do nosso post sobre cálculo, chegou a hora de usar o conhecimento. Quando dizemos que um método é analítico, significa que ele é representado por uma formula que vai nos devolver o ótimo global. Isso é possível porque o modelo linear é simples. Em geral, isso é raríssimo no mundo de machine learning. Além disso, esse é método só é possível por que a função quadrática é convexa, ou seja, possui um mínimo global, como já falamos.

Para utilizar esse método, vamos fazer uma pequena alteração na equação 8. Vamos retirar o termo \(\frac{1}{2N}\) e calcularmos apenas a soma do quadrado da diferença (daí vem o nome mínimos quadrados). Feito isso, vamos utilizar a equação na forma matricial:

\[RSS(\mathbf{w}) = (\mathbf{y} - \mathbf{w}X)^\top (\mathbf{y} - \mathbf{w} X) \tag{9}\]

Na qual \(X\) é uma matrix \(N \times k\), ou seja, cada linha \(i\) é uma entrada \(\mathbf{x}_i\); e \(\mathbf{y}\) é um array \(N \times 1\), na qual cada linha \(i\) uma saída \(y_i\) relacionada a \(x_i\). Dois pontos: o termo RSS vem do inglês residual sum of squares e para simplificar a manipulação; retiramos a notação da transposta de \(\mathbf{w}\) pois ela não afeta neste ponto, mas lembre-se que é uma multiplicação matricial. Agora, para minimizar o erro, vamos calcular a derivada do mesmo e igualar a zero. Novamente, está boiando? De uma olhada no post sobre cálculo.

\[\frac{\partial RSS(\mathbf{w})}{\partial \mathbf{w}} = X^\top (\mathbf{y}-\mathbf{w}X) \tag{10}\]

Igualando a equação 10 a zero, temos a formula que temos que solucionar para otimizar RSS:

\[X^\top (\mathbf{y}-\mathbf{w}X) = 0 \tag{11}\]

Que resulta na seguinte equação:

\[\mathbf{w} = (X^\top X)^{-1} X^\top \mathbf{y} \tag{12}\]

Essa equação é a solução analítica para o nosso problema. Ela também é conhecida como equação normal. De maneira simples, ao solucioná-la, temos os parâmetros \(\mathbf{w}\) treinados.

Obviamente, a grande vantagem dessa solução é obter a otimização em apenas um passo, ou seja, sem múltiplas iterações. Porém, nem tudo são flores. Esse método não escala muito bem. Se você possui muitas entradas, ou seja, o valor de \(N\) é muito grande, a inversão de matriz vai ser muito custoso – aproximadamente \(O(n^3)\). Por conta disso, o método mais utilizado para treinar modelos em machine learning é o do gradiente descendente, o nosso próximo tópico.

Gradiente descendente

O algoritmo do gradiente descendente (ou descida do gradiente) é o método mais comum de se otimizar modelos de machine learning. Já falamos deste método na nossa revisão de cálculo. De maneira geral, a ideia é sempre dar um passo em direção ao mínimo que a derivada aponta e iterativamente reduzir o valor do erro. Diferentemente do modelo anterior, aqui vamos dar vários passos curtos ao invés de um único. A grande vantagem é que esse método vai funcionar para grandes bases de dados e mesmo para funções que não são convexas, na qual o método pode retornar uma boa solução.

Então vamos começar a desenvolver o algoritmo. Primeiro, vamos voltar na nossa função do erro quadrático médio (MSE), descrita na equação 7, e calcular sua derivada da seguinte forma:

\[\begin{align} \frac{\partial MSE}{\partial \mathbf{w}} &= \frac{\partial}{\partial \mathbf{w}} \left ( \frac{1}{2N} \sum ( y - \hat{y} )^2 \right ) \\ &= \frac{1}{2N} \sum \frac{\partial ( y - \hat{y} )}{\partial \mathbf{w}} \\ &= \frac{1}{2N} \sum 2 ( y - \hat{y} ) \frac{\partial ( y - \hat{y} )}{\partial \mathbf{w}} \\ &= \boxed{ \frac{1}{N} \sum ( y - \hat{y} ) \frac{\partial \hat{y}}{\partial \mathbf{w}} } \end{align} \tag{13}\]

Substituindo \(\hat{y}_i = \mathbf{w}^\top \mathbf{x}_i\), e continuando a derivada, temos:

\[\begin{align} \frac{\partial MSE}{\partial \mathbf{w}} &= \frac{1}{N} \sum ( y - \mathbf{w}^\top \mathbf{x}_i ) \frac{\partial \mathbf{w}^\top \mathbf{x}_i}{\partial \mathbf{w}} \\ &= \boxed{ \frac{1}{N} \sum ( y - \mathbf{w}^\top \mathbf{x}_i ) \mathbf{x}_i } \end{align} \tag{14}\]

Excelente! Agora sabemos que a derivada do nosso erro, que aponta em direção ao mínimo, é representada pela equação 14. O próximo passo do algoritmo é definir uma regra de atualização dos parametros \(\mathbf{w}\). Para isso, fazemos:

\[\mathbf{w}^{j+1} = \mathbf{w}^{j} - \alpha \frac{1}{N} \sum ( y - \mathbf{w}^\top \mathbf{x}_i ) \mathbf{x}_i \tag{15}\]

Na qual \(\alpha\) é um parametro muito importante conhecido como taxa de aprendizagem (learning rate). De maneira simples, o que essa equação nos diz é: repita esse passo tantas vezes quanto necessário e a cada repetição atualize o valor de \(\mathbf{w}\) utilizando a derivada do erro ponderado por uma taxa que controla o quão grande essa atualização deve ser. Como o gradiente aponta para o mínimo, a taxa de aprendizado controla o quão rápido nós levamos o nosso parâmetro na direção dele. A figura a seguir ilustra essa idea.

Figura 2: ilustração do efeito da taxa de apredizagem

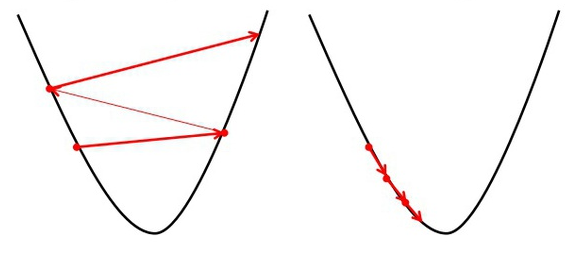
Em resumo, a figura ilustra uma função quadrática sendo minimizado. As setas vermelhas indicam o passo do parâmetro em direção ao mínimo. Na esquerda, temos uma taxa alta, o que indica que o passo será grande. Na direita, a taxa é menor, e os passos são menores. De maneira geral, um valor muito alto causa o richochete que estamos vendo na figura, equanto um valor muito pequeno pode tornar a convergência muito lenta. Logo, a pergunta natural seria: qual valor devo usar? E a melhor resposta para essa pergunta é: não sei, depende do problema. Não existe um valor mágico para taxa que vai ser bom em todos os problemas. Realmente vai depender dos dados. Esses tipos de parâmetros que são escolhidos empiricamente, e não treinados durante a otimização, são conhecidos como hiper parâmetros (hyper parameters).

Incializando os parâmetros

Se você não estiver boiando até este momento, você já entendeu que você precisa repetir a equação 15 várias vezes até encontrar o mínimo ou algo próximo a ele. Além disso, você precisa definir a taxa de aprendizagem para controlar o tamanho do passo em direção a esse mínimo. Se estamos na mesma página, outra pergunta natural seria: como eu inicializar \(\mathbf{w}\)? Bom, se vamos iterar a partir de uma posição até encontrar um mínimo, precisamos partir de algum lugar. Essa posição é escolhida aleatoriamente. Existem diversas técnicas para escolher um lugar aleatório que seja razoavelmente bom. Mas uma regra geral é utilizar uma distribuição normal. Por isso, o treinamento de algortimos de ML são conhecidos por serem estocásticos, ou seja, se treinamos duas vezes o mesmo algoritmo podemos encontrar parâmetros diferentes.

Mais uma pergunta que pode surgir: por quanto tempo devo rodar a equação 15? Mais uma pergunta que não existe resposta correta. Bem vindo a área de ML xD. Existem muitos parâmetros que são difíceis de serem escolhidos quando o modelo é grande. Mas de maneira geral, em ML, o número de iterações do gradiente é conhecido com época. Uma época, nada mais é do que executar a regra de atualização para todas as amostras do deu problema. Nesse sentido, temos que falar sobre convergência, que nada mais é do que a quantidade de épocas necessárias para o parâmetros do modelo convergir para um valor mínimo, que pode não ser o global, depende do problema. Podemos utilizar diferentes métodos para identificar quando o algoritmo convergiu. Por exemplo:

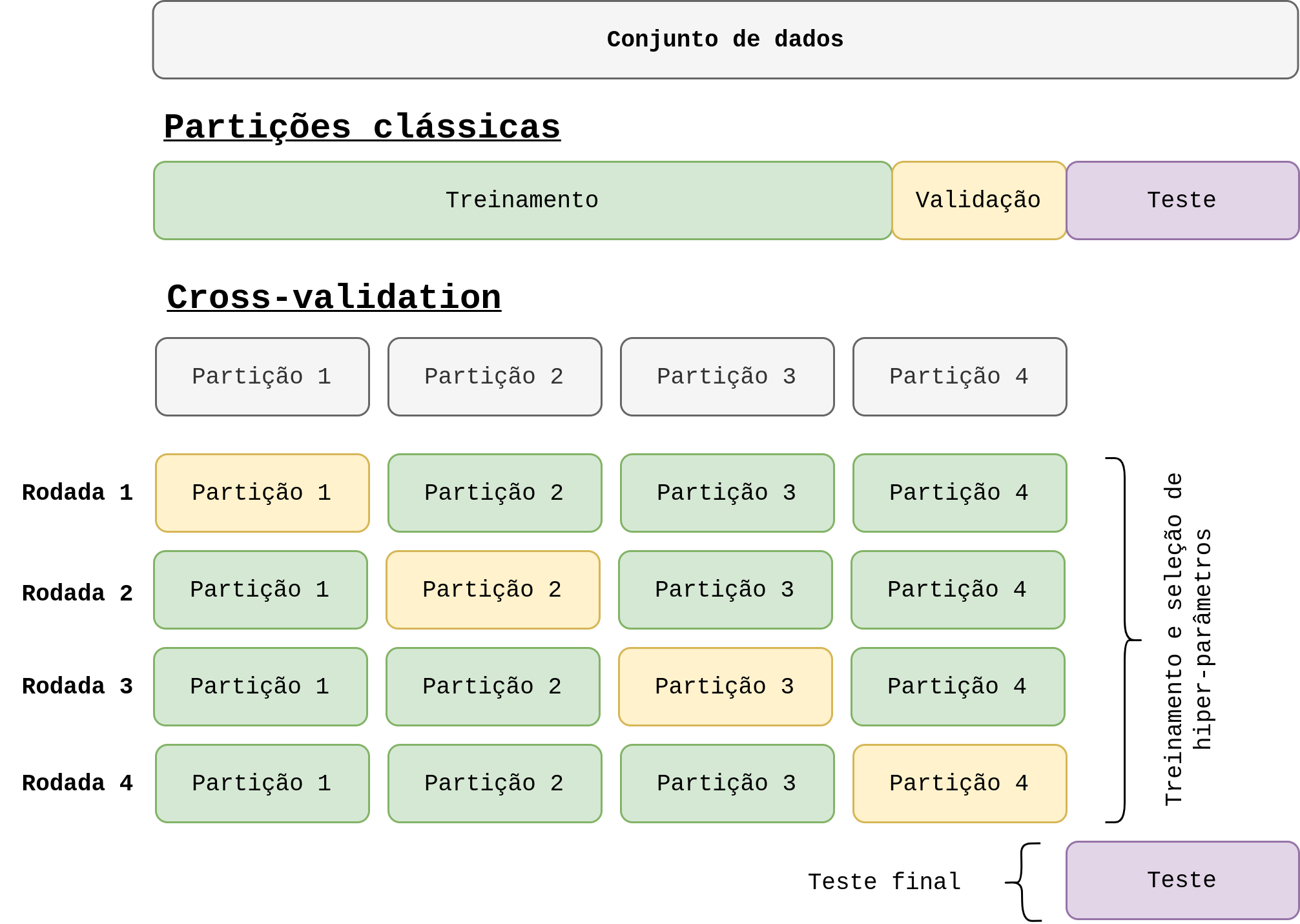
• Podemos ter um conjunto de validação na qual avaliamos a performance do modelo e quando ela parar de melhorar, significa que o algoritmo convergiu para algum lugar.
• Podemos verificar a diferença entre \(\mathbf{w}^{j+1}\) e \(\mathbf{w}^{j}\) e determinar uma tolerância mínima (por exemplo, 0.01) que quando atingida, sabemos que os parâmetros não estão atualizando mais. Neste caso eles podem estar presos em um mínimo local ou, de fato, estarem um mínimo global.

De maneira geral, devemos monitorar os hiper parâmetros durante o treinamento para garantir a qualidade do mesmo.

Melhorando o gradiente descendente

Para concluir esse post, vamos apenas introduzir uma ideia para melhorar a convergência do algoritmo. O algoritmo que definimos no momento, leva em consideração que devemos calcular o gradiente para todas as \(N\) entradas \(\mathbf{x}_i\) para performar uma atualização utilizando a equação 15. Essa ideia funciona, mas podemos melhorar. Acontece, que ela pode ter uma convergência lenta. Para melhorar um pouco, vamos adicionar um pouco mais de aleatoriedade e, além disso, vamos usar batches (a tradução dessa palavra é ruim, mas ela significa que vamos usar um grupo de entradas, ou se quiser, uma baciada de dados LoL).

A ideia é a seguinte: vamos criar diversos batches dentro da base de dados, que serão conhecidos como mini-batches, e vamos misturá-loas cada época. Para cada batch a gente vai calcular uma atualização dos parâmetros através da equação 15. Por exemplo, se \(N = 100\), ou seja, temos 100 entradas \(\mathbf{x}\), podemos divir em 10 grupos de 10 entradas. Cada grupo é um batch. Para cada batch, a gente performa um passo do gradiente. E a cada época, a gente mistura os dados para gerar batches diferentes da época anterior. Essa ideia é tão comum que tem um nome: gradiente descendente estocástico (ou stochastic gradient descent) SGD. Ela é muito utilizada em ML, mesmo para modelos bem mais complexos, e resulta em um ganho de performance muito interessante.

Considerações finais

Bom, nesse post discutimos sobre o modelo linear. Ele é o modelo mais básico em machine learning, mas importante para fixarmos os conceitos básicos. Ao longo do post fui destilando vários tópicos relevantes em ML, como convergência, inicialização de parâmentros, mini-batch etc. Fica como desafio você implementar o modelo utilizando os dois tipos de treinamento (ainda vou implementar e linkar o código aqui xD). Se você sentiu dificuldade em entender tudo, não desanime. Estude novamente e entenda o modelo. Se preciso, dê uma olhada nos posts de pré-requisitos =)

Até a próxima!

Referências

[1] James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An introduction to statistical learning. Vol. 112. New York: springer, 2013.

[2] Dive into Deep Learning: https://d2l.ai/