Machine learning pré-requistos: Cálculo

Introdução

Neste segundo post da série, vamos abordar os conceitos básicos e necessários sobre Cálculo para se iniciar na área. Este post será basicamente um apanhando geral do livro de Cálculo I e II do James Stewart. Este foi o livro que aprendi cálculo e o considero como uma excelente fonte. Existem alguns PDFs dele disponíveis por ai que você encontra no google, mas eu não sei onde encontrá-los.

Esse post será dividida em 4 partes. Na primeira, vamos fazer uma breve revisão de algumas funções. Na segunda, vamos abordar o conceito de limite. Na terceira o de derivada e na quarta Minimização/Maximização por derivadas, que é conceito mais importante o nosso propósito, ou seja, machine learning. Se você se sente confortável com os conceitos fundamentais, já vá direto para a Parte 4. Novamente, isso é um post de revisão. Para saber mais recorra as referências fornecidas.

Parte 1 - Preliminares

Antes de falar sobre limite, vamos abordar alguns conceitos que serão úteis daqui pra frente. Vou tentar ser o mais breve possível.

Função inversa

Dado uma função \(g\), a função \(f\) é definida como sua inversa se:

\[g(f(x)) = x \textrm{ e } f(g(y)) = y \textrm{, }\forall x,y \textrm{ em que } g(y) \textrm{ e } f(x) \textrm{ existem} \tag{1}\]

A notação para a essa função é \(g = f^{-1}\). Porém, cuidado para não confundir com \(a^{-1} = \frac{1}{a}\).

Calcular uma inversa é bem simples. Basta igualar uma função \(f(x) = y\) e isolar \(x\). Por exemplo, considere \(f(x) = 3 + \frac{1}{x}\). Para encontrar sua inversa fazemos \(f(x) = y\) e isolamos \(x\) da seguinte maneira:

\[3 + \frac{1}{x} = y \\ x = \frac{1}{y-3}\]

Dessa forma, \(f^{-1} = \frac{1}{y-3}\).

Função exponencial

Seja \(a\) um número positivo, fixo, chamado de base, sua exponencial é definida como:

\[a^n = a \times a \times \cdots \times a \textrm{ (n vezes) } \tag{2}\]

Algumas propriedades interessantes:

• P1: \(a^m a^n = a^{m+n}\)
• P2: \((a^m)^n = a^{mn}\)
• P3: \((ab)^n = a^{n}b^n\)

Além disso, para que a função seja definida para todos os números reais, existem as seguintes definições:

• D1: \(a^0 = 1\)
• D2: \(a^{-n} = \frac{1}{a^n}\)

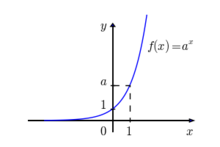
O gráfico básico de uma exponencial é exemplificado na Figura 1.

Figura 1: Gráfico básico de uma exponencial. A medida que x cresce, sua imagem y é cada vez mais amplificada. Essa é a caracteristica básica de uma exponencial. Fonte

Função logaritimica

Basicamente, o logaritmo é a função inversa da exponencial. Sendo \(a\) a base, um logartimo é definido como: \(\log_a x = z \Leftrightarrow a^z = x \tag{3}\)

Como por definição \(a^0 = 1\), temos que \(\log_a 1 = 0\) e como \(a^1 = a\), temos que \(\log_a a = 1\). Outro detalhe importante é que não existe solução para equação \(a^z = 0\). Dessa forma, \(\log_a 0\) não é definido.

Como veremos mais para frente, o logaritmo é importante para machine learning uma vez que suas propriedades auxiliam nas derivadas de algumas funções. Então, vamos as principais propriedades:

• P1: \(\log_a (xy) = \log_a x + \log_a y\)
• P2: \(\log_a x^y = y \log_a x\)
• P3: \(\log_a \frac{x}{y} = \log_a x - \log_a y\)

Além das três propropriedades acima, outra muito importante é a mudança de base:

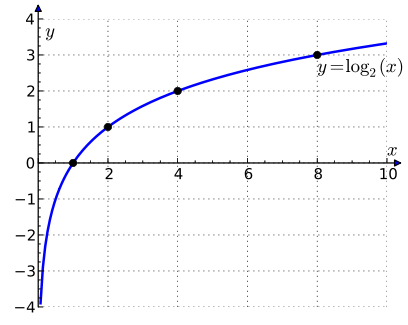
\[\log_b x = \frac{\log_a x}{\log_a b} \tag{4}\]

O gráfico básico de um logaritmo é mostrado na Figura 2.

Figura 2: Gráfico básico de um logaritmo. Observe que a curva não toca o eixo y para x=0. Como a função não é definida ali, o que temos é uma assíntota. Fonte

Logaritmo neperiano

Quando a base do logaritmo é igual a \(e = 2.718\cdots\), o logaratimo recebe o nome de neperiano ou natural. Assim como \(\pi\), \(e\) é uma constante fundamental da matemática. Dessa forma temos duas definições:

• A exponencial de \(e\) é definidade como \(e^x\)
• O logaritmo de \(e\) é definido como: \(\log_e x \rightarrow ln(x)\)

Parte 2 - Limites

Vamos começar definindo formalmente o que é limite:

Definição 1: seja \(f\) uma função definida sobre algum intervalo aberto que contém o número \(b\), exceto possivelmente no próprio \(b\), então dizemos que o limite de \(f(x)\) quando \(x\) tende a \(b\) é \(L\) se para todo número \(\epsilon > 0\) há um número correspondente \(\delta > 0\) tal que:

\[\mid f(x) - L \mid < \epsilon \textrm{ sempre que } 0 < \mid x - b \mid < \delta\]

A representação matemática do limite é descrita a seguir:

\[\lim_{x \to b} f(x) = L \tag{5}\]

Agora largando o formalismo de lado, o que essa definição nos diz é o seguinte:

• O \(\lim_{x \to b} f(x) = L\) se pudermos tornar os valores de \(f(x)\) arbitrariamente próximos de \(L\) tornando \(x\) próximo de \(b\), mas não igual a \(b\).

Definição 2: O \(\lim_{x \to b} f(x) = L\) se e somente se \(\lim_{x \to b^+} f(x) = L\) e \(\lim_{x \to b^-} f(x) = L\).

A definição 2 nos diz que aproximando \(x\) a \(b\) pela esquerda ou pela direita, o limite tem que ser o mesmo.

Limites infinitos

Pode acontecer que a medida que \(x\) se aproxima de \(b\) os valores de \(f(x)\) torna-se muito grandes. Vamos tomar como exemplo a função logaritmica definida anteriormente e plotada no gráfico da Figura 2. Portanto, tomando \(f(x) = \log_2 x\) queremos calcular o \(\lim_{x \to 0} \log_2 x\). Se observarmos a Figura 2, quanto mais o valor de \(x\) se aproxima de \(0\), o valor de \(f(x)\) se torna muito grande, mas negativo. Agora lembre-se que o logaritmo não é definido em \(0\). Nesse caso, dizemos que:

\[\lim_{x \to 0^+} \log_2 x = - \infty\]

Em outras palavras, quando o valor \(x\) se aproxima de \(0\) pela direita, mas não igualando a \(0\), o valor de \(f(x)\) tende a um número muito grande negativo, no qual chamamos de \(- \infty\). O mesmo ocorre se aproximarmos \(x\) a \(0\) pela esquerda, mas neste caso o limite tende a \(+ \infty\).

Com isso, é gerado uma assíntota, que já discutimos na parte 1 e é ilustrada na Figura 2. A curva \(f(x)\) se aproxima o quanto imaginarmos, mas jamais toca o eixo \(y\), uma vez que a função não é definida em \(0\).

Propriedades

Existem dezenas de propriedades para se calcular um limite. Como esse post é apenas uma revisão, vamos descrever apenas algumas delas. Para isso, considere \(c\) uma constante e suponha que o \(\lim_{x \to a} f(x)\) e \(\lim_{x \to a} f(x)\) existam. Sendo assim:

• P1: \(\lim_{x \to a} [f(x) \pm g(x)] = \lim_{x \to a} f(x) \pm \lim_{x \to a} g(x)\)

• P2: \(\lim_{x \to a} [cf(x)] = c \lim_{x \to a} f(x)\)

• P3: \(\lim_{x \to a} [f(x) \times g(x)] = \lim_{x \to a} f(x) \times \lim_{x \to a} g(x)\)

• P4: \(\lim_{x \to a} [f(x) \div g(x)] = \lim_{x \to a} f(x) \div \lim_{x \to a} g(x)\) se \(\lim_{x \to a} g(x) \neq 0\)

• P5: \(\lim_{x \to a} [f(x)]^n = [\lim_{x \to a} f(x)]^n\)

• P6: \(\lim_{x \to a} \sqrt[n]{f(x)} = sqrt[n]{\lim_{x \to a} f(x)}\)

• P7: \(\lim_{x \to a} c = c\)

• P8: \(\lim_{x \to a} x^n = a^n\)

Portanto, essas definições são extremamente úteis para se calcular o limite de uma função.

Regra da substituição direta

Um das regras mais úteis para se calcular limite é o da substituição direta. Juntamente com as propriedades anteriores, somos capazes de calcular o limite de uma grande gama de funções. Mas antes de definir a regra, precisamos definir continuidade.

Definição 3: Uma função \(f(x)\) é contínua em \(a\) se:

\[\lim_{x \to a} f(x) = f(a)\]

Da mesma forma, \(f(x)\) é contínua a direita se \(\lim_{x \to a^+} f(x) = f(a)\) e a esquerda se \(\lim_{x \to a^-} f(x) = f(a)\). Por fim, \(f(x)\) é contínua em um intervalo se a função é contínua para todos os pontos deste intervalo.

Para complementar a definição 3, existe o seguinte teorema:

Teorema 1: os seguintes tipos de função são contínuas em todo número de seus domínios:

• Polinômio
• Funções racionais
• Funções raízes
• Funções exponenciais
• Funções trigonométricas
• Funções logaritmimicas
• Funções trigonométricas inversas

Agora vamos a definição da regra da substituição direta, que é bem simples:

Portanto, a partir da definição e do teorema acima, temo as regra da subsituição direta, ou seja, caso \(f(x)\) seja contínua em \(a\), para calcular o limite de \(x \to a\) basta calcular \(f(a)\).

Cálculo da reta tangente

Dado o gráfico obtido pela equação \(y = f(x)\), se quisermos encontrar a reta tangente a curva em um ponto \(P(x_0, f(x_0))\), fazemos o seguinte:

• Definir a reta tangente \(t\) de inclinação \(m\) que passa por \(P\)
• Considerar um ponto vizinho \(Q(x, f(x))\), com \(x \neq a\)
• Calcular a inclinação da curva \(PQ\) da seguinte forma (da álgebra linear do ensino médio):

\[m_{PQ} = \frac{f(x) - f(a)}{x-a} \tag{6}\]

Ao traçar a reta \(PQ\) obtemos uma reta secante a curva \(y\). A ideia é mover essa curva até ela se tornar uma tangente no ponto \(P\). A Figura 3 ilustra essa operação.

Figura 3: Estratégia para cálculo da reta tangente a partir da reta secante. Fonte

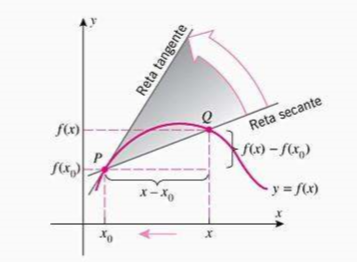
• Para executar essa estratégia precisamos fazer \(Q\) se aproximar de \(P\). Para isso fazemos \(x \to x_0\).
• Se \(m_{PQ} \to m\), então a tangente \(t\) será a reta que passa em \(P\) com inclinação \(m\).
• Isso implica que a reta tangente é a posição limite da reta secante, como ilustrado no gráfico.

De acordo com os passos acima, podemos definir a reta tangente da seguinte forma:

Definição 4: A reta tangente a uma curva \(y = f(x)\) em um ponto \(P(a, f(a))\) é a reta que passa por \(P\) com inclinação:

\[m = \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \tag{7}\]

Desde que o limite exista. Também é comum encontrar a equação 7 da seguinte forma:

\[m = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \rightarrow h = x - a \tag{8}\]

Neste momento você pode está se perguntando: mas pra que estou lendo sobre cálculo da reta tangente em um curso de machine learning? Bom, esse é o passo inicial para a compreensão de derivadas, o que é fundamental no universo de ML. Na verdade, a equação 8 é tão comum na ciência e engenharia que ela ganhou um nome especial: derivada. A inclinação da reta tangente no ponto \(P\) é a interpretação geométrica do que é derivada. Isso abre caminho para última parte deste post.

Parte 3 - Derivadas

A definição de derivada é basicamente a mesma da definação 4. Mas de qualquer forma:

Definição 5: a derivada de uma função \(f\) em um número \(a\), denotada por \(f'(a)\) ou \(\frac{d(fa)}{da}\) é definida como:

\[f'(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \rightarrow h = x - a \tag{9}\]

se o limite existir.

A interpretação geométrica da derivada nós já sabemos, ou seja, a inclinação da reta tangente no ponto \((a, f(a))\). Porém, a interpretação mais importante é como taxa de variação.

Derivada como taxa de variação

A derivada pode ser interpretada como a taxa de variação instântanea de \(y=f(x)\) em relação a \(x\) quando \(x = a\).

Vamos definir a taxa de variação instântanea de \(y = f(x)\) em relação a \(x\) em \(x=x_1\). Se o intervalor for \([x_1, x_2]\), então a variação \(\Delta x = x_2 - x_1\) é correspondente em \(y\) como \(\Delta y = f(x_2)-f(x_1)\). Com isso, a taxa de variação instântanea é cálculada da seguinte forma:

\[t = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{x_1 \to x_2} \frac{f(x_2)-f(x_1)}{x_2 - x_1} \tag{10}\]

Com isso, a derivada \(\frac{d f(a)}{da}\) é a taxa de variação instântanea de \(y = f(x)\) em relação a \(x\) quando \(x = a\).

Funções diferenciáveis

Nem toda função é diferenciável e isso é importante em machine learning. Por isso temos o seguinte teorema:

Teorema 2: se \(f(x)\) é diferenciável em \(x = a\), então \(f\) é contínua neste ponto.

Este teorema está de acordo com a definição 3. Porém, atenção! A recíproca não é verdadeira! Por exemplo, a função \(f(x) = \mid x \mid\) é contínua, porém ela não é diferenciável em \(0\), uma vez que não é possível calcular a reta tangente a este ponto.

De maneira geral, você pode considerar que se uma curva \(y = f(x)\) muda abruptamente de direção, formando uma quina, uma dobra ou uma tangente vertical, a função não é diferenciável no ponto pois não terá tangente.

Regras de diferenciação

Nesta subseção vamos apresentar as principais regras de diferenciação até a regra da cadeia, que é de extrema importância para machine learning. Lembrando que isso é apenas uma revisão, para provas e versões completas, recorra a referência disponibilizada. Para facilitar a escrita, considerando a \(\frac{dq(x)}{dx}\) como \(q'(x)\), sendo \(q(x)\) uma função diferenciável, temos as seguintes regras:

• Constante: \(f'(c) = 0\)
• Multiplicação por constante: \([c f(x)]' = cf'(x)\)
• Função potência: \(f'(x^n) = nx^{n-1}\)
• Regra da soma/diferença: \([f(x) \pm g(x)]' = f'(x) \pm g'(x)\)
• Regra do produto: \([f(x) g(x)]' = f'(x)g(x) + f(x)g'(x)\)
• Regra do quociente: \([\frac{f(x)}{g(x)}]' = \frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}\)

Obviamente podemos compor essas regras para obtermos as derivadas desejadas. Mais pra frente teremos alguns exemplos.

Derivadas de algumas funções especiais

Algumas funções são bem frequentes, como as trigonométricas e logaritmicas. As derivadas dessas funções são definidas como:

• Derivada de \(e^x\): \([e^x]' = e^x\)
• Derivadas trigonométricas:
  • Seno: \([sen(x)]' = cos(x)\)
  • Cosseno: \([cos(x)]' = -sen(x)\)
  • Tangente: \([tg(x)]' = sen^2(x)\)
• Derivada de funções logaritmica
  • Base \(a\): \([\log_a x]' = \frac{1}{x \ln a}\)
  • Base \(e\): \([\log x]' = \frac{1}{x}\)

  O Interessante das derivadas logaritmicas é que ela pode ser usada para facilitar derivadas complicadas. Obviamente isso é utilizado em machine learning. Por exemplo, considere \(y = \frac{x^{3/4} \sqrt{x^2 + 1}}{(3x + 2)^5}\). A primeira vista, calcular essa derivada parece muito difícil! Mas vamos aplicar \(\ln\) em ambos os lados da equação e em seguida aplicar as regras anteriormente definidas:

  \[\ln y = \ln \left ( \frac{x^{3/4} \sqrt{x^2 + 1}}{(3x + 2)^5} \right ) \\ \ln y = \ln(x^{3/4}) + \ln(\sqrt{x^2+1})-5(\ln 3x + \ln 2) \because \textrm{ Regras de log} \\ \ln y = 3/4 \ln x + 1/2 \ln(x^2 + 1) - 5(\ln 3x + \ln 2) \because \textrm{ Regras de log} \\ \frac{1}{y}y' = \frac{3}{4} \frac{1}{x} \frac{1}{2} \frac{1}{x² + 1} 2x - 5 \frac{1}{3x} 3 + \frac{1}{2} \because \textrm{ Regras de dif.} \\ y' = y \left( \frac{3}{4x} + \frac{x}{x^2 + 1} - \frac{15}{3x + 2} \right ) \because \textrm{ Substituir y} \\\]

Regra da cadeia

A regra da cadeia é, talvez, a mais importante regra de diferenciação e é parte fundamental do backpropagation, que você vai ouvir falar muito ainda. Logo, vamos definí-la:

Definição 5: Seja \(f(x)\) e \(g(x)\) duas funções diferenciáveis e seja \(F = f(g(x))\), então \(F'\) é definida como: \(F'(x) = f'(g(x))g'(x) \tag{12}\)

A regra também é encontrada na seguinte notação: seja \(y = f(u)\) e \(u = g(x)\), então:

\[\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} \tag{13}\]

• Exemplo 1: Calcular deriva de \(F(x) = \sqrt{x^2 + 1}\).
  1. Primeiramente, manipulando a função: \(F(x) = {x^2 + 1}^{1/2}\)
  2. Aplicando a regra da cadeia e as regras de diferenciação: \(F'(x) = 1/2(x^2 + 1)^{-1/2}(2x) = x(x^2 + 1)^{-1/2}\)
• Exemplo 2: Calcular deriva de \(F(x) = cos(x^2)\).
  1. Aplicando a regra da cadeia: \(F'(x) = 2x (cos(x^2))\)

Derivadas superiores

Até o momento, foi aprensentado derivadas de primeira ordem. Porém, podemos ter derivadas de 1ª, 2ª, 3ª etc ordens. Portanto, se uma função \(f(x)\) é diferenciável, \(f'(x)\) também é uma função, logo, pode ter sua própria derivadas \((f'(x))'\). Essa derivada é chamada de derivada segunda:

\[\frac{d}{dx} \frac{dy}{dx} = \frac{d^2 y}{dx^2} \tag{14}\]

Derivadas parciais

Até o momento tratamos de função de uma variável, no caso \(f(x)\). Porém, podemos ter funções de mais de uma variável, por exemplo, \(f(x,y)\). É muito comum desejarmos calcular a derivada desse tipo de função. Quando isso ocorre, chamamos essa derivada de derivada parcial, e você vai entender o motivo em instantes.

Primeiramente, é importante pontuar que a derivada parcial seguem os mesmos princípios da derivada de uma variável. Portanto, vamos seguir as mesmas regras, porém, com duas variáveis. A interpretação também é idêntica aos postulados anteriores, obviamente, levando em consideração as duas variáveis.

O importante aqui é entender que, para duas variáveis, teremos duas derivadas, uma com respeito a \(x\) e outra a \(y\). Para mais variáveis é a mesma ideia. Por isso a ideia de parcial, não temos um único valor, mas parcelas. A notação utilizada é:

• Derivada parcial de \(f(x,y)\) com respeito a \(x\) : \(\frac{\partial f(x,y)}{\partial x}\)
• Derivada parcial de \(f(x,y)\) com respeito a \(y\) : \(\frac{\partial f(x,y)}{\partial y}\)

A regra geral para deterinar as derivadas parciais de uma função \(z = f(x,y)\) é muito simples e é definida 2 passos:

1. Para calcular \(\frac{\partial f(x,y)}{\partial x}\), olhe para \(y\) como uma constante e derive a função \(f(x,y)\) normalmente com respeito a \(x\)

2. Para calcular \(\frac{\partial f(x,y)}{\partial y}\), olhe para \(x\) como uma constante e derive a função \(f(x,y)\) normalmente com respeito a \(y\)

• Exemplo: calcular as derivadas parciais de \(f(x,y) = 2x + y^2\)
  1. Com respeito a \(x\) : \(\frac{\partial f(x,y)}{\partial x} = 2\)
  2. Com respeito a \(y\) : \(\frac{\partial f(x,y)}{\partial y} = 2y\)

Parte 4 - Maximização/Minimização via derivadas

Essa parte é a mais importante do post pois será extremamente utilizada nos algoritmos de minimização de redes neurais. Para iniciar o tema, vamos definir o teorema de Fermat que é fundamental para que a mágica aconteça:

Teorema 3: Se uma função \(f(x)\) tiver um máximo ou um mínimo local em \(c\) e \(f'(c)\) existir, então \(f'(c) = 0\).

Em outras palavras, o teorema diz que ao igualar a derivada de uma função a zero, estamos encontrando os mínimos e máximos dessa função. Porém, o inverso do teorema não se aplica. Por exemplo, lembra da função \(\mid x \mid\), ela possui mínimo em \(0\), porém, como já discutimos, a derivada não existe neste ponto.

Sendo assim, para encontrar os valores de máximo e mínimo absolutos de uma função contínua \(f(x)\) em um intervalo \([a,b]\), basta seguir os seguintes passos:

1. Determinar o(s) ponto(s) na(s) qual(is) a \(f'(x) = 0\) em \([a,b]\).
2. Calcular os valores de \(f(x)\) nos extremos do intervalo
3. O maior valor calculado nos passos anteriores é o máximo absoluto e o menor o mínimo absoluto.

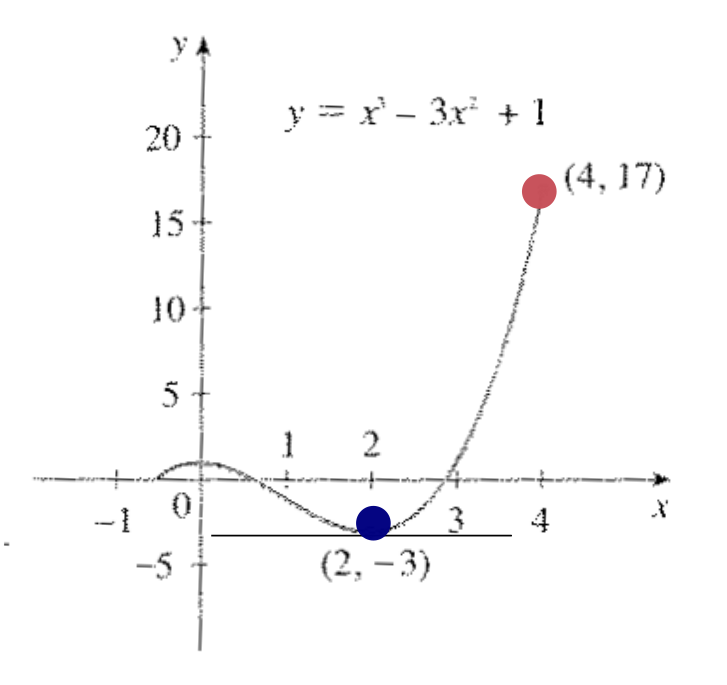
• Exemplo: calcular os valores do máximo e mínimos global de \(f(x) = x^3 - 3x^2 + 1\) no intervalo \([\frac{-1}{2}, 4]\).
  1. Derivando: \(f'(x) = 3x^2 - 6x = \underline{3x(x - 2)}\)
     • Fazendo \(f'(x) = 0\), encontramos os pontos \(x= 0\) e \(x = 2\).
  2. Calculando os valores extremos: \(f(-1/2) = 1/8\) e \(f(4) = 17\)
  3. O ponto de máximo é \((4,17)\) e o de mínimo \((2,-3)\).

Se observarmos o gráfico da função na Figura 4, podemos ver o máximo e o mínimo. Além disso, caso a derivada exista, a reta tangente ao máximo ou ao mínimo é horizontal. Podemos observar isso no ponto \((2,-3)\).

Figura 4: Gráfico da que mostra o mínimo (azul) e máximo (vermelho) global da função no intervalo desejado Fonte

Derivadas direcionais e vetor gradiente

Nesta seção vamos falar um pouco da derivada direcional, que é utilizada para determinar a taxa de de variação de uma função de duas ou mais variáveis em qualquer direção.

Da definição de variável, dado \(z = f(x,y)\), sabemos que as derivadas parcias \(\frac{\partial z}{\partial x}\) e \(\frac{\partial z}{\partial y}\) representam as taxas de variação de \(z\) na direção positiva dos eixos \(x\) e \(y\), que também pode ser interpretada como na direção e sentido dos versores \(\vec{i}\) e \(\vec{j}\).

Para iniciar, vamos supor que desejamos calcular a taxa de variação de \(z\) no ponto \((x_0, y_0)\) na direção e sentido de um vetor unitário arbitrário \(\vec{u} = \left \langle a, b \right \rangle\). Isso é ilustrado na seguinte figura:

Figura 5: representação do vetor u. Fonte

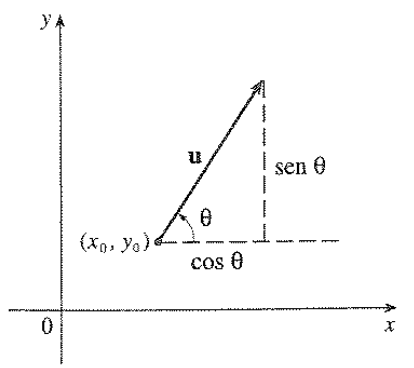
Agora considere a superfície 3D \(S\) que é gerada a partir de \(z = f(x,y)\) e \(z_0 = f(x_0, y_0)\). O ponto \(P(x_0, y_0, z_0)\) pertence a \(S\). O plano vertical que passa por \(P\) na direção de \(\vec{u}\) intercepta \(S\) em uma curva \(C\). A inclinação da reta tangente \(T\) a \(C\) em \(P\) é a taxa de variação de \(z\) na direção e sentido de \(\vec{u}\). Para calcular essa taxa, é utilizada a mesma estratégia descrita na parte 2 deste post, porém baseado em 2 variáveis. Dessa forma, vamos descrever apenas o teorema resultado de todas essa manipulação matemática.

Teorema 4: se \(f(x,y)\) é uma função diferenciável em \(x\) e \(y\), então essa função possui uma derivada direcional de direção e sentido de qualquer versor de \(\vec{u} = \left \langle a, b \right \rangle\) e:

\[D_u f(x,y) = \frac{\partial z}{\partial x}a + \frac{\partial z}{\partial x}b \tag{15}\]

Baseado neste teorema, podemos escrever a derivada direcional como produto escalar de dois vetores:

\[D_u f(x,y) = \left \langle \frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial x} \right \rangle \left \langle a,b \right \rangle \\ D_u f(x,y) = \left \langle \frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial x} \right \rangle \vec{u} \tag{16}\]

O primeiro vetor é tão importante que recebeu um nome especial: gradiente.

Definição 6: seja \(f(x,y)\) uma função no \(\mathbb{R}^2\), o gradiente de \(f\) é a função vetorial \(\nabla f(x,y)\) definida por:

\[\nabla f(x,y) = \frac{\partial f(x,y)}{\partial x}\vec{i} + \frac{\partial f(x,y)}{\partial x} \vec{j} \tag{17}\]

Para funções no \(\mathbb{R}^n\), basta adicionar as variáveis no somatório da equação 17.

Por fim, vamos ao último teorema deste post, mas que é de suma importância:

Teorema 5: seja \(f\) uma função diferenciável no \(\mathbb{R}^n\), o valor máximo da derivada direcional é \(\mid \nabla f(\vec{x}) \mid\) e ocorre quando \(\vec{u}\) tem a mesma direção e sentido que o vetor gradiente \(\nabla f(\vec{x})\).

Em outras palavras, esse teorema nos diz que a função \(f\) aumenta mais depressa na direção e sentido do gradiente \(\nabla f\). Isso é um resultado muito importante! Significa que se desejarmos maximizar uma determinada função, o gradiente da mesma aponta para o valor máximo! E obviamente, se eu inverter a direção deste vetor, ele vai apontar para o mínimo! Isso é exaustivamente utilizado em machine learning e vamos utilizar esse resultado diretamente muito breve!

Considerações finais

Essa foi mais um dos posts teóricos que podem até ser chatas, mas são importantes para formar a base necessária para área. No fundo, machine learning é isso, quanto mais você cava, mais matemática você encontra. Como bem disse Dijkstra (se você não sabe que é, faça o dever de casa), “Ciência da computação tem tanto a ver com o computador como a Astronomia com o telescópio, a Biologia com o microscópio, ou a Química com os tubos de ensaio. A Ciência não estuda ferramentas, mas o que fazemos e o que descobrimos com elas.”