O problema de otimização

Introdução

Problemas de otimização são aqueles que visam determinar o pontos extremos de uma função, seja ele mínimo, e então os problemas serão de minimização, ou máximo, problemas de maximização. Otimização é algo extremamente comum em nosso cotidiano. Os exemplos vão desde os mais simples, como pegar um caminho mais curto para chegar no trabalho, escolher os produtos corretos no supermercado para diminuir o preço da compra; até problemas mais complexos, como minimizar custos de uma produção em uma fábrica, determinar o melhor conjunto de rotas para uma transportadora, dentre diversos outros.

A otimização abrange as mais diversas áreas do conhecimento, problemas de engenharia, de biologia, de economia/administração, etc, e seja qual for o problema e a área, o primeiro passo rumo a otimização do mesmo é a modelagem matemática. A otimização necessita de uma função matemática para atuar e muita das vezes, principalmente em sistemas dinâmicos, a modelagem não é tarefa simples. Por isso, esta é uma área da engenharia. Este post não tem a intenção de discutir como modelar um sistema, portanto já partimos do princípio que o problema é modelado e sua função é conhecida.

Função objetivo

A modelagem do sistema, no problema de otimização, é representado pela função objetivo, também conhecida como fitness ou aptidão. Essa é a função que desejamos minimizar ou maximizar. Essa função pode ser simples, como por exemplo uma função de duas dimensões \((x,y)\), ou até funções mais complexas com \(n\) dimensão, como mostra a Figura 1.

Figura 1: Funções obejtivos. (a) Duas dimensões (b) Mais de duas dimensões

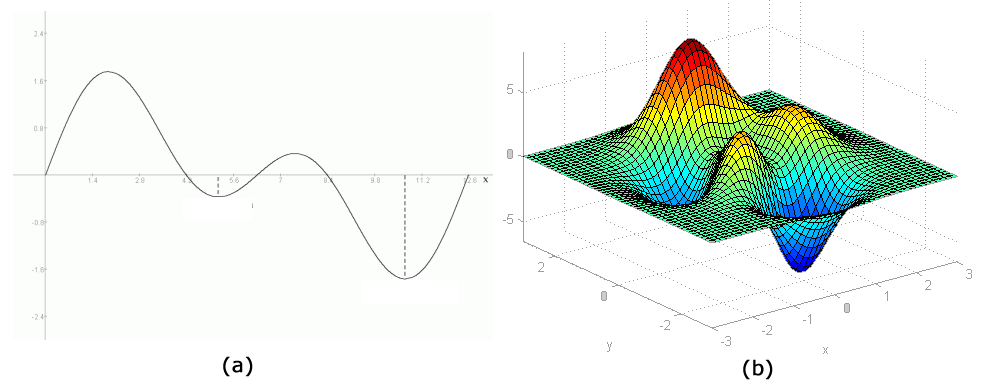
Além disso, um dos grande desafios na otimização são as funções multimodais, que são aquelas que em sua curva possuem diversos mínimos e/ou máximos locais. Na Figura 2 é mostrado uma função multimodal 2D (a função é 2D para facilitar a visualização). Perceba que a função possui diversas cristas e vales. Suponhamos que o nosso desejo seja minimizar essa função, ou seja, encontrar em qual ponto dela o valor é mínimo. Bom, em nossa imagem ele esta demarcado com um ponto verde. Esse ponto é a solução ótima para o problema. Os demais pontos vermelhos são mínimos locais e eles dificultam algoritmos de otimização a encontrar a solução ótima. O mesmo se aplica para problemas de maximização.

Figura 2: uma função 2D multimodal

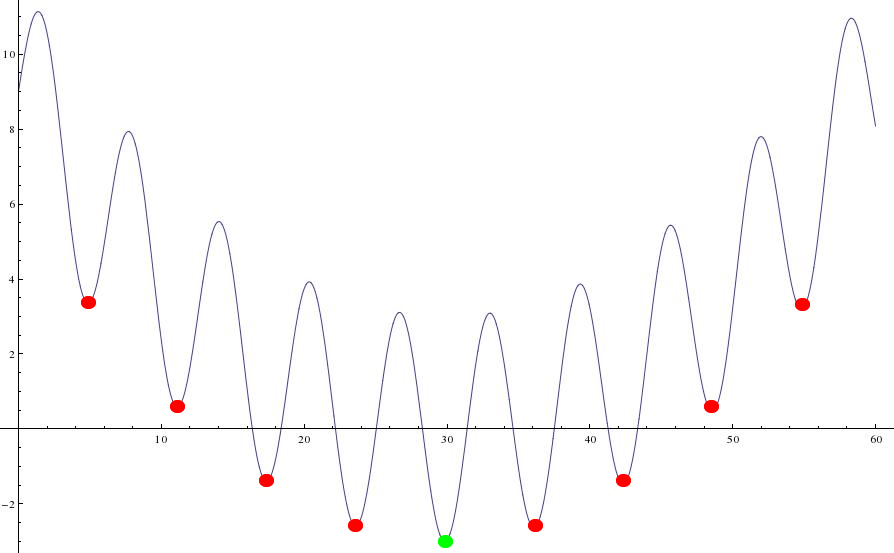
Áreas de otimização

Dentro da grande área de otimização existem outras sub-áreas, de acordo com o tipo de problema. Existem problemas de otimização linear, que são os mais fáceis e é possível obter a solução ótima, e problemas não lineares, que são os mais difíceis e em muitos deles é complicado garantir uma solução ótima. Também podemos dividir os problemas de otimização em contínuos, aqueles que as variáveis são contínuas, e otimização inteira, no qual o objetivo é encontrar um variável inteira. Além disso, o problema pode ter restrições ou não. Problemas com restrições são aqueles em que o universo de busca, como por exemplo, nossas curvas das Figuras 1 e 2, são restritos. Significa que existem pontos em que o a solução não cabe no problema e isso é mais uma complicação para se obter o ótimo global.

Algoritmos de otimização

Existem diversos algoritmos de otimização, para os mais variados tipos de problemas. Dentre eles podemos destacar:

• Simplex: utilizado para otimizar somente problemas lineares, com ou sem restrição. Garante a solução ótima para o problema, mas por outro lado, a maioria esmagadora dos problemas do mundo real é não linear.

• PSO - particle swarm optimization: Algoritmo heurístico utilizado para otimizar qualquer tipo de função, com ou sem restrições (é preciso adaptar o algoritmo para isso). Não garante a solução ótima do problema, mas garante uma boa solução. Para mais informações, acesse o post sobre o PSO neste blog.

• Algoritmo Genético - GA Segue o mesmo princípio do PSO. Também é heurístico, para qualquer tipo de problema e não garante o ótimo. Você também pode conferir o post sobre o GA neste link.

• DE - differential evolution: Da mesma família que o GA e com as mesmas características. Também já escrevemos sobre o DE, acesse aqui.

• Gradiente descendente: Algoritmo baseado em derivadas. Utilizado em otimizações não lineares. Possui um ponto fraco de cair em mínimos locais de maneira fácil.

• Simulated anneling: Fundamentado na termodinâmica, também é uma heurística para problemas não lineareas.

• Nelder-Mead: Também uma heurística utilizada para funções não lineares e principalmente quando as derivadas não podem ser computadas.

Esses são apenas alguns exemplos, existem diversos outros algoritmos de otimização e cada um tem suas próprias qualidades, deficiências e características.

Exemplo de função objetivo para otimização

Um exemplo de função objetivo não linear para otimização é mostrado abaixo:

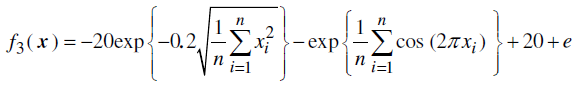
Esta é uma função que pode ter dimensão \(n\) e é um benchmark para testar se um algoritmo de otimização é eficaz. Além disso, pode ser inclusas restrições, limitando o espaço de busca de \(x\). Essa função é usada para minimização.

Por falar em minimização, caso você implemente um algoritmo de minimização, para converter o problema para otimização bastar utilizar o negativo da função objetivo, ou seja, \(min [f(x)] = max [-f(x)]\).

Exemplo de problema de otimização - O problema do caixeiro viajante

Um dos problemas clássicos na área de otimização é o problema do caixeiro viajante. Todo aluno iniciante na área de computação certamente já ouviu falar dele. A formulação do problema é simples, mas sua solução extremamente complexa de acordo com o que o número de cidades cresce.

Formulação do problema

Imagine que você seja um caixeiro que realiza entregas em \(N\) cidades. Para economizar no combustível e no tempo, seu objetivo é simples: encontrar a menor rota para visitar as \(N\) cidades, visitando uma única vez cada uma delas, e retornar à cidade de origem.

Figura 3: O problema do caixeiro viajante

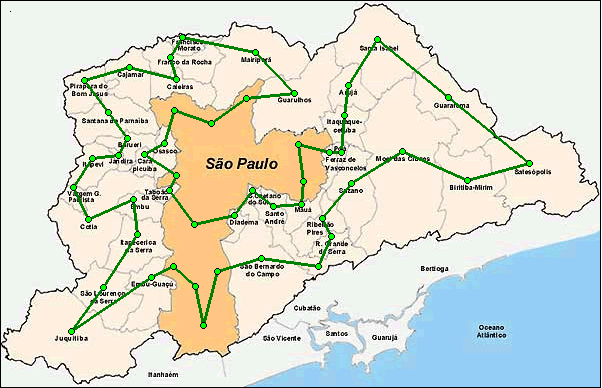
Caso queira saber mais sobre o problema, assista o video abaixo que descreve de maneira didática e leve a complexidade do problema.