O algoritmo Differential Evolution - DE

Introdução

O algoritmo Differential Evolution (DE - em português Evolução Diferencial) foi proposto por Storn e Price, em 1997 [1]. e é um método heurístico, que não usa derivadas, e visa solucionar problemas de otimização contínua.

Desde de sua criação, o DE se apresenta como um simples, mas poderoso algoritmo de otimização numérica para busca da solução ótima global, sendo aplicado com sucesso na solução de vários problemas de otimização difícil. Segundo Cheng e Hwang [2], o DE, possui como principais características:

• É um algoritmo de busca estocástica, originado dos mecanismos de seleção natural;
• O algoritmo é simples e de fácil entendimento,com poucos parâmetros de controle para conduzir à otimização;
• É eficaz para solucionar problemas de otimização com função objetivo descontínua, pois não necessita de informações sobre derivadas da mesma;
• Manipula uma população de soluções que utiliza diferentes regiões no espaço de busca, tornando o algoritmo robusto a mínimos locais;
• É eficaz mesmo trabalhando com uma população pequena;
• Permite as variáveis serem otimizadas como números reais, sem processamento extra;

Conceitos básicos

População

O primeiro conceito do DE, assim como o de outros algoritmos evolutivos, é o de população. Uma população é composta por N indivíduos, também chamados de vetores, cobrindo todo espaço de busca, para um problema com n variáveis de projeto, ou seja, a dimensão de cada vetor. De maneira geral, a população será simplesmente uma matriz N x n, na qual cada linha da matriz representa um indivíduo da população. Um exemplo de uma população com 3 indivíduos de dimensão 5 é descrito na matriz abaixo:

\[populacao = \begin{bmatrix} 1.0 & 2.6 & 3.7 & 3.1 & 7.7\\ 4.4 & 6.2 & 7.4 & 8.8 & 5.1 \\ 3.2 & 8.3 & 9.1 & 7.7 & 6.1 \\ \end{bmatrix} \tag{1}\]

Normalmente, a população é criada por uma distribuição de probabilidade uniforme. Caso exista informações prévias sobre o problema, a inicialização pode ser diferente, vai variar para cada caso.

Uma vez criada a população, a mesma é submetida a ação de operadores evolutivos, ou seja, o DE começa a atuar de fato. É importante ressaltar que o número de indivíduos é fixado durante todo o processo de otimização. Portanto, dado uma população, os três operadores a serem executados são: mutação, cruzamento e seleção. Essas três operações serão repetidas até que um critério de parada seja alcançado. Esse critério pode ser convergência da população, um erro mínimo atingido ou um valor pré-definido de iterações. Observe que a ideia é similar a um algoritmo genético! Sendo assim, os operadores do DE se baseiam no princípio da evolução natural cujos os principais objetivos são:

• Manter a diversidade da população;
• Evitar convergências prematuras;
• Obter a melhor solução para o problema;

Obviamente o algoritmo não garante o ótimo, mas sim soluções muito próximas deles, dependendo do problema, é claro.

Operações do DE

A seguir são descritos detalhadamente cada uma das operações do algoritmo.

Mutação

Na operação de mutação são escolhidos, de maneira aleatória, três indivíduos distintos dentre todos os N que compões a da população inicial. Para facilitar a compreensão, vamos nomear cada um deles. A população inicial será \(pop_O\) (de população original) e seus indivíduos escolhidos aleatoriamente serão:  \(I_\alpha, I_\beta\) e \(I_\gamma\).

O indivíduo  \(I_\alpha\) sofre uma pertubação resultante da diferença vetorial entre \(I_\beta\) e \(I_\gamma\). Essa diferenção é multiplica por um fator \(F\) conhecido como fator de mutação. Esse operador gera uma nova população de indivíduos mutados, que vamos chamar de \(pop_M\) (de população mutada). Tudo isso é resumido na seguinte expressão:

\[popMut = I_\alpha + F \times I_\beta - I_\gamma \tag{2}\]

Na qual, \(\alpha, \beta, \gamma \in (1 , 2 , ..N)\) e \(\alpha \neq \beta \neq \gamma\). Vale ressaltar que para garantir as diferenças entre os indivíduos selecionados aleatoriamente, a população deverá ser igual ou superior a 4 indivíduos. Além disso, o fator de mutação \(F\), que controla a amplitude da diferença vetorial, deve está no intervalo entre 0.5 e 1 [1]. A Figura 1 ilustra a operação de mutação:

Figura 1: Ilustração da operação de mutação. Neste exemplo, a população possui 8 indivíduos e foram escolhidos aleatoriamente os indivíduos 1, 4 e 7 para realizar a operação

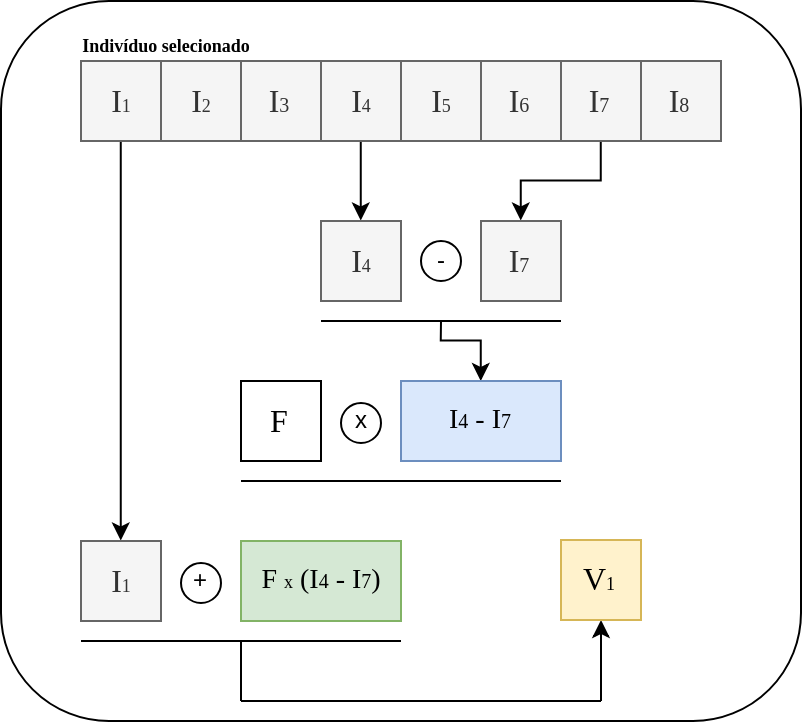
Portanto, em resumo, a mutação gera uma nova população, que chamamos de \(pop_M\) a, a partir da população originar \(pop_O\)

Cruzamento

Com intuito de aumentar a diversidade da população, Storn e Price [1] introduziram o operador de cruzamento. Essa operação é usada para gerar um novo indivíduo advindo de um cruzamento entre indivíduos da população original e da população mutada. Para melhor compreensão imagine você e seus pais. Você é um indivíduo que surgiu através do cruzamento dos genes de seu pai e de sua mãe. A ideia é parecida aqui.

Ao fim dessa operação, todos os indivíduos cruzados formarão uma nova população que chamaremos de \(pop_C\) (de população de cruzamento) de mesmo tamanho e dimensão das populações obtidas anteriormente.

Para ficar bem didático e fácil de compreender, imagine o primeiro indivíduo da população \(pop_C\), vamos chamá-lo de \(I_c\). Ele vai ser composto pelo cruzamento, de um indivíduo da \(pop_O\), \(I_o\), e outro indivíduo da \(pop_M\), \(I_m\), ambos selecionados de maneira aleatória. Esses indivíduos possuem dimensão n (lembre-se da matriz que discutimos no início do post, na qual cada linha é um novo indivíduo, ou seja, um vetor [1,n]) e vamos chamar cada uma dessas n posições de genes. Por exemplo, se o individuo é um vetor de dimensão 5, v = [1 2 3 4 5], ele possui 5 genes, um pra cada posição de v, entendido?

A ideia é cruzar os genes dos indivíduos \(I_o\) e \(I_m\) para gerar o indivíduo \(I_c\). Então, imagine: \(I_c = [4, 4, 4, 4]\) e \(I_m = [5, 5, 5, 5]\), um indivíduo \(I_c\) possível é igual a \([4, 5, 4, 5]\), na qual os genes 1 e 3 são de \(I_c\) e 2 e 4 são de \(I_m\). Para decidir qual gene é transmitido existe uma taxa de cruzamento \(C_r\), definida no intervalo [0.8, 1] [1]. Para gerar essa taxa, sorteia-se um número aleatório, \(rand\), e verifica: se \(C_r\) for maior do que \(rand\), o gene mutante é transmitido, caso contrário, o gene da população corrente é passado adiante. Então observe, no exemplo com \(I_c = [4, 4, 4, 4]\) e \(I_m = [5, 5, 5, 5]\), o número aleatório é sorteado 4 vezes e verificado qual gene deve ser transmitido para \(I_c\). Poratanto, para o gene 1, \(rand\) foi maior do que \(C_r\), então passa o gene 1 de \(I_c\). Para o gene 2, \(C_r\) foi maior do que \(rand\), então passa o gene 2 de \(I_m\) e assim por diante.

Tudo isso que discutimos foi realizado para gerar apenas um indivíduo da \(pop_C\), ideia é continuar para os N indivíduos. A expressão a seguir ilustra o cruzamento:

\[I_C^{ij} = I_M^{ij} \texttt{ se } rand_{j} \leq Cr \texttt{ ou } j=k \\ I_C^{ij} = I_O^{ij} \texttt{, caso contrário } \tag{3}\]

Na qual, \((i=1 ... N), (j=1...n), (k=1...N) \texttt{ e } rand_{i} \in [0,1]\). O índice \(k\) é um parâmetro escolhido para cada indivíduo com objetivo de dar garantia de que ao menos um gene do indivíduo mutante seja copiado para o indivíduo cruzado. Portanto, se o número aleatório for menor que a taxa de cruzamento ou se o índice \(k\) for igual ao índice \(j\), o gene do indivíduo cruzado será proveniente do indivíduo mutante. Caso contrário, o gene será proveniente do indivíduo original. A Figura 2 ilustra essa operação.

Figura 2: Ilustração da operação de cruzamento.

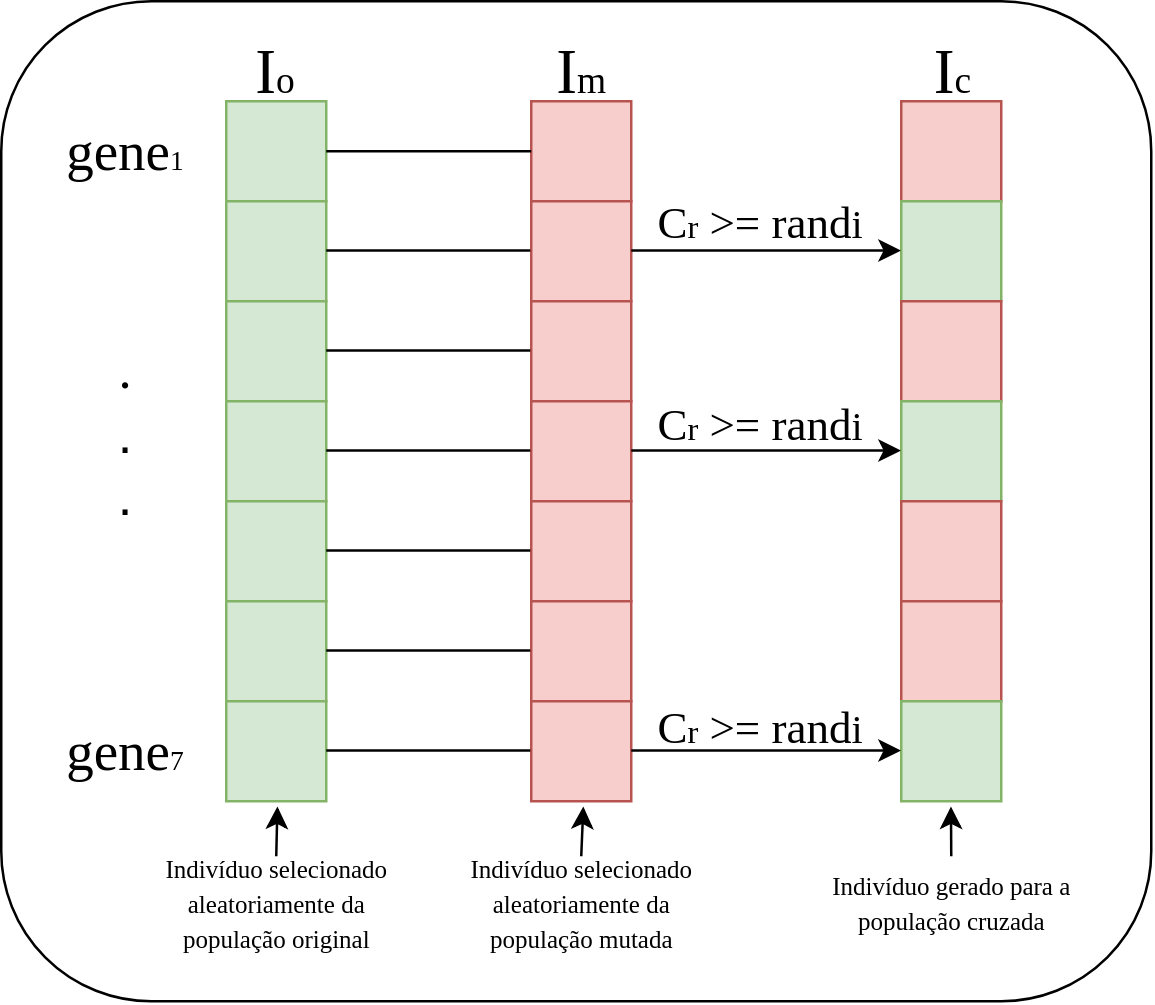
Seleção

Por fim é realizada a operação de seleção. Mas para falar de seleção, antes temos que conhecer a função objetivo, também conhecida como fitness. A fitness é a função que pretendemos otimizar (minimizar ou maximizar). Então, vamos supor que desejamos otimizar a função seno, com isso nossa fitness \(f(x) = sen (x)\). Sendo assim, ela será nossa função de avaliação, de onde será gerado um erro. Se o intuito é minimizar, sabemos que o mínimo que a função seno pode atingir é -1, com isso a otimização caminhará para esse valor ao longo das iterações, e toda população (nesse caso unidimensional, pois só existe um gene em cada indivíduo) vai ser avaliada pela função seno. Quanto mais longe de -1, menos apto é aquele indivíduo.

Sabendo o que é uma função objetivo, o operador de seleção visa simplesmente escolher, dentre a população corrente e a população cruzada, os melhores indivíduos. É uma verificação simples. Se a fitness do indivíduo \(i\) da \(pop_O\) é maior do que a fitness do indivíduo \(i\) da \(pop_C\), esse indivíduo passa para próxima geração, que será chamada de \(pop_B\) (de população best, ou seja, melhor), como mostra a expressão a seguir.

\[pop_B^i = pop_C^{i} \texttt{ se } f(pop_O^{i}) \leq f(pop_C^{i}) \\ pop_B^i \texttt{, caso contrario } \tag{4}\]

Sendo $f$ a função de fitness.

Sendo assim, os indivíduos mais aptos são passados para a próxima geração, formando a população dos melhores indíviduos. No caso do seno, os indivíduos mais aptos são aquels com valores próximos de -1. Com isso, é finalizada uma iteração do algoritmos. Na próxima iteração, a \(pop_O\) será igualada a \(pop_B\) e todo o processo é realizado novamente até que um critério de parada seja atingido, como ilustra a Figura 3. Ao final de todo o processo, basta escolher o indíviduo da \(pop_B\) que possua o melhor valor na avaliação da função de fitness.

Figura 3: Fluxograma do Differential Evolution.

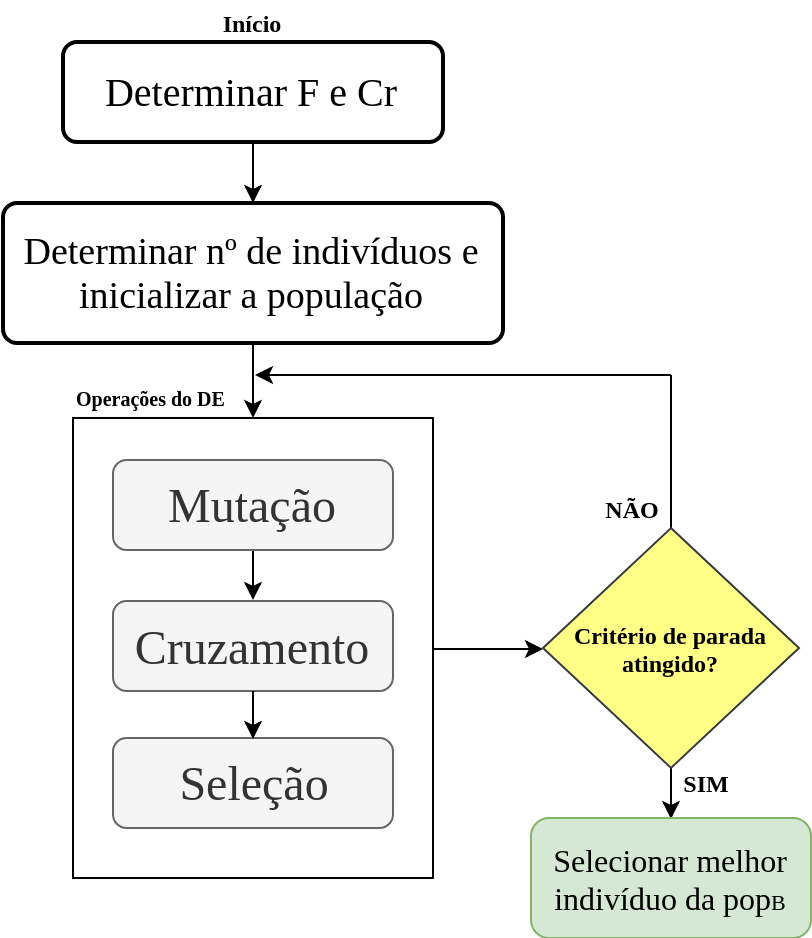
Uma observação importante: o que define se a seleção escolhe o indivíduo com maior ou menor fitness é o tipo de otimização. Se for maximização escolhe-se o maior e se for minimização escolhe-se o menor.

Código exemplo

Para finalizar, deixo o link do meu repositório do Github de uma simples implementação do differential evolution. A implementação foi feita em MATLAB e possui diversos comentários para auxiliar o entendimento. Sinta-se livre para utilizar o código, mas lembre-se de dar os devidos créditos.

Caso encontre algum bug ou tenha alguma sugestão, não exite em entrar em contato comigo. Até a próxima!

Referências

[1] STORN, R.; PRICE, K. Differential evolution - A simple and efficient heuristic for global optimization over continuous spaces. J. Global Optimiz, v. 11, pp. 341–359, 1997.

[2] CHENG, S. L.; HWANG, C. Optimal approximation of linear systems by a differential evolution algorithm, IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, v. 31, n. 6, pp. 698-707, 2001’