Fundamentos da lógica fuzzy

Introdução

Os conjuntos fuzzy foram inicialmente propostos por Zadeh em 1965 [1] como uma extensão da teoria clássica de Conjuntos e, desde então, tem sido utilizada nas mais diversas áreas, tai como: tomada de decisão [2], clusterização [3], predição de séries temporais [4], dentre diversas outras.

A lógica clássica x lógica fuzzy

Na lógica clássica, o valor verdade de uma proposição assumirá somente dois valores: Verdadeiro (1) ou Falso (0), não havendo outra possibilidade. Além disso, os predicados são termos exatos como: igual a, maior que, menor que, etc. Portanto, os elementos de um conjunto \(A\) em determinado universo \(X\) simplesmente pertencem ou não àquele conjunto. Isso pode ser descrito pela seguinte função:

\[f_A = \left\{\begin{matrix} 1 & \textrm{se e somente se} x \in A \\ 0 & \textrm{se e somente se} x \notin A \end{matrix}\right. \tag{1}\]

Na lógica fuzzy, o valor verdade de uma proposição pode assumir uma infinidade de proposições, chamadas de expressões linguísticas, interpretadas como subconjuntos fuzzy em um intervalo \([0, 1]\). Os predicados, definidos aqui, são termos subjetivos e imprecisos, como: quente, frio, alto, gordo. Sendo assim, o uso da lógica fuzzy é aconselhada para problemas em que a informação seja de natureza imprecisa ou incompleta, tornando assim, mais fácil a incorporação de conhecimento ao sistema, pois fornece um modo para um especialista traduzir o seu conhecimento sem uma abordagem matemática. 

Definições básicas

A seguir são apresentadas as definições básicas acerca da lógica fuzzy.

Definição 1. Um conjunto fuzzy \(A\) do universo de discurso \(U\), é caracterizado por uma função de pertinência \(\mu: U \rightarrow [1,0]\). Essa função associa a cada elemento de \(x\) de \(U\) o grau \(\mu(x)\), com a qual \(x\) pertence ao conjunto \(A\) [1].

Sendo assim, a partir da Definição 1, pode-se concluir que a função de pertinência \(\mu(x)\) indica o grau de compatibilidade entre \(x\) e o conceito expresso por \(A\).

• \(\mu(x) = 1\) indica que \(x\) é completamente compatível com \(A\).
• \(\mu(x) = 0\) indica que \(x\) é completamente incompatível com \(A\).
• \(0 < \mu(x) < 1\) indica que \(x\) é parcialmente compatível com \(A\), com grau de pertinência \(\mu(x)\).

Portanto, um conjunto \(A\) da lógica clássica pode ser visto como um conjunto fuzzy específico, denominado usualmente como crisp, na qual o grau de pertinência é do tipo “tudo ou nada”, e não gradual como nos conjuntos fuzzy. A lógica clássica esta contida na lógica fuzzy.

Definição 2. Uma variável linguística é uma entidade utilizada para representar de modo impreciso (linguístico) um conceito ou uma variável de um dado problema. Admite-se como valores expressões linguísticas que, por sua vez, são representados por conjuntos fuzzy existentes no universo \(U\) [1].

Um pouco mais tarde, em 1987, Zadeh propôs uma caracterização mais ampla, fazendo com que a passagem da pertinência para não pertinência fosse mais lenta e gradual, na medida em que os elementos são mais pertinentes à um conjunto do que à outros. Com isso, a função de pertinência de uma conjunto \(A\), pode ser expressada de diversas formas, tais como: triangular, trapezoidal, gaussiana, exponencial, dentre outras, como mostrado na Figura 1.

Figura 1: Formas comuns utilizada para função de pertinência na lógica fuzzy

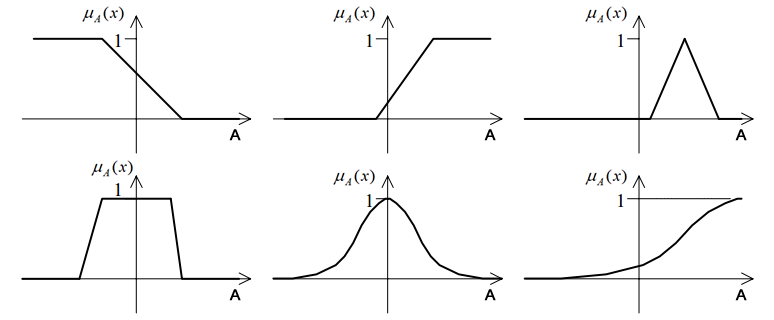
Exemplo de utilização

Se você é iniciante neste assunto e/ou não se da bem com definições lógicas e afins, preparei um pequeno exemplo para maior compreensão do que foi exposto até aqui (normalmente aprendemos mais com exemplos do que com definições, pelo menos comigo funciona melhor rs). Imagine o seguinte diálogo entre os famosos Joãozinho e Zezinho:

• Z: Nossa Joãozinho você viu aquele carro que passou correndo na rua?
• J: Sim. Será qual a velocidade dele?
• Z: Acho que por volta de uns 100 km/h.

Observe que no simples diálogo Zezinho utilizou um rótulo, por volta de uns 100 km/h, para expressar a velocidade de um carro para Joãozinho. Expressões como esta nós utilizamos diariamente para expressar uma infinidade de eventos. Fica claro que uma pessoa só responderia Joãozinho com exatidão se tivesse em mãos um velocímetro, sem ele a resposta é sempre incerta.

Bom, seguindo em frente, a expressão por volta de uns 100 km/h  pode ser modelada por uma função de pertinência triangular, como ilustar a Figura 2. 

Figura 2: Função de pertinência para variável linguística velocidade no exemplo anterior.

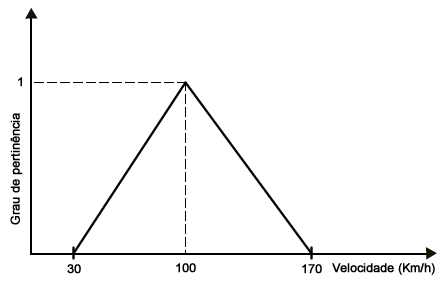
Os valores maiores e menores que 100 km/h são distribuídos, com grau de pertinência máximo em 100 km/h, sugerindo a ideia de que quanto mais próximo desta velocidade, mais o valor se identifica com o rótulo proposto por Joãozinho. O mesmo conjunto também pode ser modelado para qualquer uma das formas ilustradas na Figura 1, isso é simplesmente uma opção de projeto.

De maneira geral, conceitos humanos são expressos de forma qualitativa, como: “por volta de”, “aproximadamente”, “levemente”, “mais ou menos”, ao invés de valores quantitativos. Elementos qualitativos podem ser representados por meio de variáveis linguísticas, as quais assumem valores dentro de um conjunto de termos linguísticos. Retornando ao exemplo da representação da velocidade como variável linguística, esta pode assumir rótulos como: muito Baixa (MB), baixa (B), média (M), alta (A), muito alta (MA). Para atribuir significado aos termos linguísticos, associa-se cada um deles a um conjunto fuzzy, sobre um mesmo universo de discurso e definido com base na experiência ou intuição de um ser humano, como mostra a Figura 3.

Figura 3: universo de discurso da variável linguística velocidade e seus possíveis rótulos.

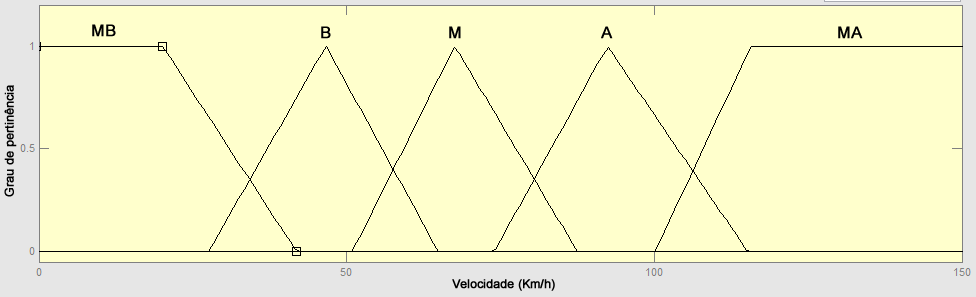
A principal função das variáveis linguísticas é fornecer uma maneira sistemática para uma caracterização aproximada de fenômenos complexos ou mal definidos. Em essência, a utilização do tipo de descrição linguística empregada por seres humanos, e não de variáveis quantificadas, permite o tratamento de sistemas que são muito complexos para serem analisados através de modelos matemáticos convencionais.

Espero que este artigo tenha sido útil de alguma forma. Em um próximo post vou apresentar uma implementação, em MATLAB e Python, de operações entre números fuzzy triagulares e trapezoidais. Até a próxima.

Referências

[1] Zadeh, L. A., Fuzzy Sets, Information and Control, v. 8, p. 338-353, 1956.

[2] Krohling, Renato A., André GC Pacheco, and André LT Siviero. “IF-TODIM: An intuitionistic fuzzy TODIM to multi-criteria decision making.” Knowledge-Based Systems 53 (2013): 142-146.

[3] Ghaffarian S., Ghaffarian S. Automatic histogram-based fuzzy C-means clustering for remote sensing imagery. ISPRS Journal of Photogrammetry and Remote Sensing\r\nv. 97, p. 46–57, 2014.

[4] Chen, S.M. Forecasting enrollments based on fuzzy time series. Fuzzy Sets Systems, Elsevier North-Holland, Inc., v. 81, n. 3, p. 311–319, 1996.