K vizinhos mais próximos - KNN

Introdução

Após um pequeno hiato no blog, hoje vamos falar um pouco sobre um dos classificadores clássicos mais conhecidos, o K vizinhos mais próximos (do inglês: K-nearest neighboors – KNN). O KNN foi proposto por Fukunaga e Narendra em 1975 [1]. É um dos classificadores mais simples de ser implementado, de fácil compreensão e ainda hoje pode obter bons resultados dependendo de sua aplicação. Antes de iniciar, caso você não tenha afinidade com o problema de classificação, sugiro que leia nosso post sobre classificação de dados. Agora, sem mais delongas, vamos ao que interessa.

Funcionamento do KNN

A ideia principal do KNN é determinar o rótulo de classificação de uma amostra baseado nas amostras vizinhas advindas de um conjunto de treinamento. Nada melhor do que um exemplo para explicar o fucionamento do algoritmo como o da Figura 1, na qual temos um problema de classificação com dois rótulos de classe e com \(k = 7\). No exemplo, são aferidas as distâncias de uma nova amostra, representada por uma estrela, às demais amostras de treinamento, representadas pelas bolinhas azuis e amarelas. A variável \(k\) representa a quatidade de vizinhos mais próximos que serão utilizados para averiguar de qual classe a nova amostra pertence. Com isso, das sete amostras de treinamento mais próximas da nova amostra, 4 são do rótulo \(A\) e 3 do rótulo \(B\). Portanto, como existem mais vizinhos do rótulo \(A\), a nova amostra receberá o mesmo rótulo deles, ou seja, \(A\).

Figura 1: exemplo de classificação do KNN com dois rótulos de classe e k = 7

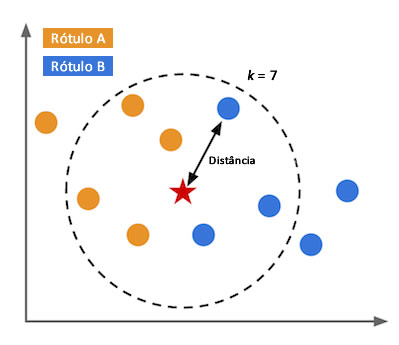
Dois pontos chaves que devem ser determinados para aplicação do KNN são: a métrica de distância e o valor de \(k\). Portanto, vamos discutir cada uma delas.

Cálculo da distância

Calcular a distância é fundamental para o KNN. Existem diversas métricas de distância, e a escolha de qual usar varia de acordo com o problema. A mais utilizada é a distância Euclidiana, descrita pela equação 1.

\[D_E(\mathbf{p},\mathbf{q}) = \sqrt{(p_1 - q_1)^2 + \cdots + (p_n - q_n)^2} = \sqrt{\sum_{i=1}^n (p_i - q_i)^2} \tag{1}\]

Outros exemplos de distância, é a de Minkowsky:

\[D_M(\mathbf{p},\mathbf{q})= \begin{pmatrix} \sum_{i=1}^n |p_i-q_i|^r \end{pmatrix}^\frac{1}{r} \tag{2}\]

E também, a distância de Chebyshev:

\[D_C(\mathbf{p},\mathbf{q}) = max_i(|p_i, q_i|) \tag{3}\]

Em todos os casos, \(\mathbf{p} = (p_1, \cdots, p_n)\) e \(\mathbf{q} = (q_1, \cdots, q_n)\) são dois pontos \(n\)-dimensionais e na equação 2, \(r\) é uma constante que deve ser escolhida. No exemplo da Figura 1, essas distâncias seriam calculadas entre as bolinhas (azuis e laranjas) e a estrela (a nova entrada). Como o exemplo é 2D, cada uma cada ponto teria seu valor em \(x\) e em \(y\). Para problemas com dimensões maiores a abordagem é a exatamente a mesma, porém, a visualização das amostras no espaço é mais complicada.

A escolha de K

Em relação a escolha do valor \(k\), não existe um valor único para a constante, a mesma varia de acordo com a base de dados. É recomendável sempre utilizar valores ímpares/primos, mas o valor ótimo varia de acordo com a base de dados. Dependendo do seu problema, você pode utilizar um algoritmo de otimização (PSO, GA, DE etc) para encontrar o melhor valor para o seu problema. Todavia, você pode deixar o desempenho geral do modelo bem lento na etapa de seleção de \(k\). Outra maneira e simplesmente testar um conjunto de valores e encontrar o valor de \(k\) empiricamente.

Pseudocódigo

Para melhor compreensão do algoritmo, apresento também o pseudocódigo do mesmo:

Código do KNN em Python

Resumidamente, a grande vantagem do KNN é sua abordagem simples de ser compreendida e implementada. Todavia, calcular distância é tarefa custosa e caso o problema possua grande número de amostras o algoritmo pode consumir muito tempo computacional. Além disso, o método é sensível à escolha do \(K\).

Por fim, deixo linkado uma implementação do KNN em Python. No meu repositório do Github:

• Implementação do KNN em Python

Caso esse código seja útil para você, considere deixar a sua estrelinha no repositório!

Referências

[1] Fukunaga, K.; Narendra, P. M. A branch and bound algorithm for computing k-nearest neighbors. IEEE Transactions on Computers, v. 100, n. 7, p. 750–753, 1975.