A máquina de aprendizado extremo - ELM

Introdução

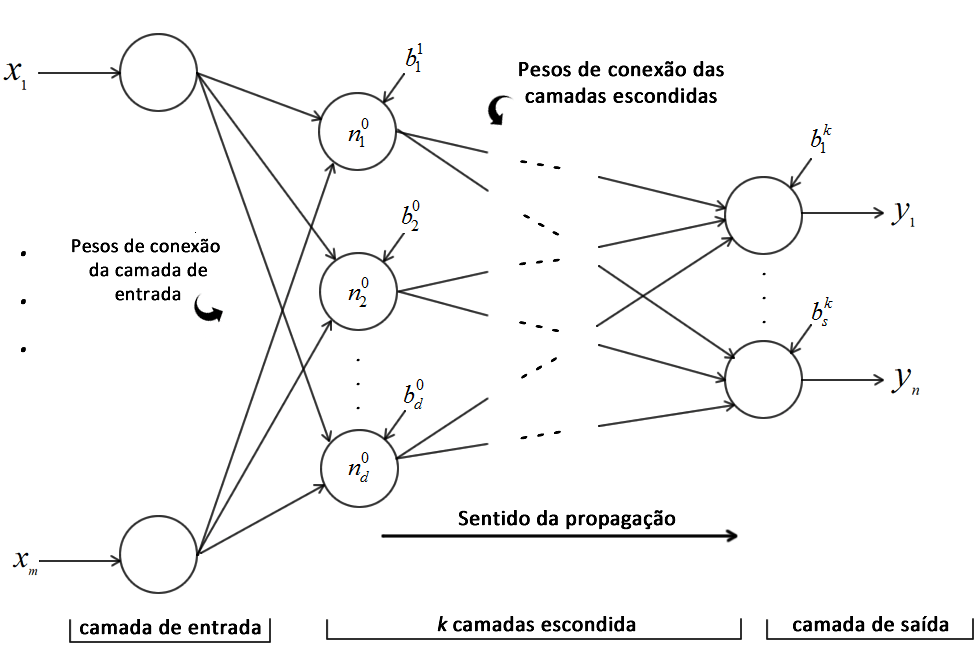
Hoje vamos apresentar a Máquina de Aprendizado Extremo(do inglês: Extreme Learning Machine, ELM), algoritmo proposto por Huang et al. [1,2] e que nada mais é do que uma maneira diferente de treinar uma rede neural artificial (RNA) de apenas uma camada oculta. O princípio de funcionamento da ELM é o mesmo de uma RNA, todavia a metodologia de treinamento de uma ELM não é baseada em gradiente descendente. Com isso o algoritmo escapa das principais deficiências do backpropagation: convergência lenta e convergência para mínimos locais. Segundo Huand et al. [2] o treinamento de uma ELM pode ser milhares de vezes mais rápido do que o treinamento via backpropagation (e muitas das vezes, de fato é). Para ilustras a arquitetura de uma ELM, podemos utilizar a mesma figura do post de RNA, porém com k = 1, ou seja, temos apenas uma camada oculta.

Figura 1: A ELM nada mais é do que uma RNA com apenas uma camada oculta, ou seja, k = 1

Modelagem matemática

Observando a Figura 1, o vetor \(X\) é a entrada da rede. Os pesos de conexão da camada de entrada são alocados em uma matriz denominada \(W\) e já os da camada oculta em uma matriz denominada \(\beta\). Para facilitar e agilizar os cálculos, os bias dos neurônios da camada oculta também são alocados na última linha de \(W\), e os bias da camada de saída não são utilizados na ELM. A modelagem matricial do ELM é descrita a seguir:

\[\mathbf{X} = [x_1, \cdots, x_m, 1] \qquad \mathbf{W} = \begin{bmatrix} w_{11}& \cdots & w_{1d} \\ \vdots & \ddots & \vdots \\ w_{m1}& \cdots & w_{md} \\ b_1 & \cdots & b_d \end{bmatrix} \tag{1}\] \[\boldsymbol{\beta} = \begin{bmatrix} \beta_{11}& \cdots & \beta_{1s} \\ \vdots & \ddots & \vdots \\ \beta_{d1}& \cdots & \beta_{ds} \end{bmatrix} \qquad \mathbf{Y} = [y_1, \cdots , y_s] \tag{2}\]

Sendo, \(m\) é o número de neurônios de entradas, \(d\) é o número de neurônios na camada oculta e \(s\) é o número de neurônios de saída da rede.

Treinamento da ELM

O treinamento da ELM é realizado de maneira analítica, diferentemente da abordagem iterativa do backpropagation. A matriz \(W\) é gerada de maneira aleatória e não é alterada até o fim do algoritmo. Essa matriz pode ser gerada de uma distribuição uniforme no intervalo [-1,1]. Portanto, o objetivo do treinamento da ELM é encontrar a matriz de pesos \(\beta\), baseado na matriz de saída \(Y\) e na matriz de pesos aleatórios \(W\), por meio da resolução de um sistema linear.

Derterminando a matriz H

Após inicializar a matriz de pesos aleatoriamente, o próximo passo é determinar a matriz \(H\) da seguinte maneira:

\[\mathbf{H}^i = [x^i_1, \cdots, x^i_m, 1] \times \begin{bmatrix} w_{11}& \cdots & w_{1d} \\ \vdots & \ddots & \vdots \\ w_{m1}& \cdots & w_{md} \\ b_1 & \cdots & b_d \end{bmatrix} \Rightarrow \mathbf{H} = \begin{bmatrix} f(H^1)\\ f(H^2) \\ \vdots\\ f(H^N) \end{bmatrix}_{N \times d} \tag{3}\]

Na qual a função \(f(.)\) é a função de transferência (pode ser uma sigmoid, por exemplo) da camada e \(i = \{1, \cdots, N\}\), sendo \(N\) o número de amostras do conjunto de treinamento. Portanto, a matriz \(\mathbf{H}\) armazena o resultado de todos os neurônios da camada oculta obtidos a partir da multiplicação entre \(\mathbf{X}\) e \(\mathbf{W}\). Observe que essa multiplicação nada mais é do que a forma matricial do neurônio perceptron, que já foi descrito no post de redes neurais. Além disso, observe que os bias foram adicionados na última linha da matriz de pesos e, por conta disso, no array de entrada \(X\), é adicionado uma coluna de 1. Isso nada mais é do que uma jogada matemática que agiliza a computação e facilita a implementação. Caso mão tenha entendido, retire os bias da matriz de peso e a coluna de 1 do array de entrada, efetue a multiplicação \(X \times W\) e na sequência some com \(b\). O resultado é o mesmo!

Determinando a matriz de features \(\beta\)

Uma vez determinada a matriz \(H\), para se obter os pesos da matriz \(\boldsymbol{\beta}\) deve ser solucionado o seguinte sistema linear:

\[\mathbf{H} \boldsymbol{\beta} = \mathbf{Y} \rightarrow \boldsymbol{\beta} = \mathbf{H}^\dagger \mathbf{Y} \tag{4}\]

Na qual \(\mathbf{H}^\dagger\) é a inversa generalizada de Moore–Penrose [3] da matriz \(\mathbf{H}\). Caso fosse utilizado a inversa padrão, o algoritmos seria limitado a problemas que essa inversa existisse. A inversa generalizada ‘afrouxa’ algumas exigências da inversa tradicional, como por exemplo, a matriz não precisa ser quadrada. Para mais informações, consulte [3]. (Para quem usa Python+Numpy e/ou MATLAB, é o comando pinv(), já implementado nas bibliotecas de algebra linear).

Por fim, vale a pena ressaltar que a matriz \(\beta\) é conhecida como matriz de features porque ela guarda as informações extraídas pela rede. Como a ELM possui apenas uma camada oculta, essa é a única informação “útil” que a rede armazena, uma vez que os pesos da camada de entrada é calculado de maneira aleatória.

Limitações e outras versões da ELM

Bom, realizado os passos acima a rede está treinada e pode ser executada. Observe, que devido ao fato do treinamento da ELM ser executado de forma analítica, o mesmo é realizado de maneira mais rápida do que um método iterativo [2]. Todavia a abordagem possui suas fraquezas. A primeira delas é relacionada a inicialização aleatória dos pesos da matriz \(\mathbf{W}\). Pode ocorrer dos valores obtidos para \(\mathbf{W}\) desencadear, ao fim do processo, em uma matriz \(\boldsymbol{\beta}\) que proporcione um resultado final ruim. Outro ponto é que a matriz \(H\) pode ser singular, ou seja, não é possível encontrar uma matriz inversa para a mesma. Por conta disso, Huang et al. [2] propõe algumas técnicas para que isso seja evitado. Além disso, o cálculo da inversa generalizada pode ser custoso se a rede possui muitos neurônios na camada oculta e muitas entradas na base de dados. Por conta disso, existe uma versão do algoritmo chamado Online Sequential ELM. Em breve farei um post discutindo esse algoritmo, aguarde.

Existem diversos trabalhos que visam otimizar a escolha dos valores de \(\mathbf{W}\) por meio do uso de algoritmos evolutivos como o GA [4], por exemplo. Por fim, a rede realmente obtém bons resultados e pode ser milhares de vezes mais rápida do que uma rede neural tradicional. Obviamente, isso sempre vai depender do seu problema.

Código em Python e MATLAB

Para você testar o algoritmo, deixo linjado o código do mesmo em Python e MATLAB. Caso encontre algum bug ou tenha alguma sugestão, sinta-se livre para entrar em contato. Faça bom uso!

• Código ELM em python
• Código ELM em MATLAB

Referências

[1] Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: a new learning scheme of feedforward neural networks. IEEE International Joint Conference on Neural Networks, v. 2, p. 985–990, 2004.

[2] Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: theory and applications. Neurocomputing, v. 70, n. 1, p. 489–501, 2006

[3] Serre, D. Matrices: theory and applications. New York: Springer, 2002.

[4] Han, F.; Yao, H.-F.; Ling, Q.-H. An improved evolutionary extreme learning machine based on particle swarm optimization. Neurocomputing, v. 116, p. 87–93, 2013.