Machine learning pré-requistos: Teoria da probabilidade

Em mais um post da série de pré-requisitos, vamos abordar os conceitos básicos e necessários sobre probabilidade e teoria da informação. Um dos pilares de machine learning é probabilidade. Os algoritmos são, em sua maior parte, estocásticos e fortemente baseados em estatística. Portanto, esse post também é muito importante para se iniciar no assunto. Esse post é fortemente baseada em três livros que deixo linkado nas referências. Lembrando, que isso é uma revisão do básico necessário. Para mais informações, recorra as referências.

Introdução

De maneira geral, a teoria de probabilidade é um conjunto de regras, axiomas e teoremas matemáticos para representar incerteza. Fenômenos incertos ocorrem a todo momento. O mundo real é incerto. Por exemplo, a previsão do tempo é um modelo probabilístico. Existe uma probabilidade de determinado evento ocorrer, por exemplo, chover, e a teoria da probabilidade nos oferece um ferramental para modelar esses eventos incertos. Por outro lado, a teoria da informação nos permite a quantificar essas incertezas. Por conta disso, ambas teorias são importantíssimas em diversas áreas da ciência e engenharia. Em machine learning não é diferente, uma vez que os algoritmos aprendem a partir dos dados, certamente os modelos também serão incertos, uma vez que é extramente complicado (para não dizer impossível) modelar o mundo real perfeitamente. Neste caso, a incerteza é gerada pois o modelo é incompleto. Um exemplos simples é quando discretizamos um sinal contínuo. Ao fazer isso, estamos descartando informações, o que gera imprecisão.

É importante ressaltar que o fato de um modelo ser probabilistico definitivamente não quer dizer que ele é ruim. Na verdade, em muitos casos é mais prático ter um modelo simples mas incerto do que uma regra extramamente complexa e certa. Tomando o exemplo utilizado em [1], imagine a seguinte regra: a maioria dos pássaros voam. Ela é simples e serve para uma gama enorme de passáros. Mas ela incerta, pois sabemos que existe exceções. Uma opção a mesma, seria: pássaros voam, exceto os que ainda não aprenderam, os machucados, Ema, Avestruz etc. Essa seria uma regra certa, mas extremamente complexa de modelar e manter.

Probabilidade frequentista e Bayesiana

A teoria da probabilidade foi originalmente criada para analizar frequência de eventos. Por exemplo, o famoso exemplo de lançar uma moeda para obter cara ou coroa. É claro que a probilidade de cada evento é 50%. Isso significa que se a repetirmos esse experimento, ou seja, jogar uma moeda para cima, uma quantidade de vezes muito grande a quantidade de vezes que se obtem cara ou coroa vai convergir para o valor de 50%. Esse tipo de probabilidade é conhecida como frequentista.

Por outro lado, existem certos problemas que essa caractrística de repetição não ocorre. Se você vai em um médico e ele diz que você tem 60% de chance de ter uma doença X, essa probabilidade significa algo diferente. Não é possível fazer varias replicas de sua pessoa para repetir os seus sintomas e verificar que você está com X. Neste caso, a probabilidade que o médico informa é um grau de confiança, na qual 100% representa certeza que você está com a doença X e 0% que não está. Esse tipo de probabilidade é conhecida como Bayesiana.

Probabilidade

Vamos começar definido probabilidade e três conceitos básicos que serão muito importantes ao longo do nosso curso: probabilidade condicional, conjunta e marginal.

Definição

Para definir probabilidade, vamos considerar um experimento com um conjunto de resultados \(\Omega\). Esse experimento pode ser o famoso exemplo de rolar um dado (um padrão, não um de RPG rs), que gera um conjunto \(\Omega\) com seis resultados possíveis, \(\{\omega_1, \omega_2, \omega_3, \omega_4, \omega_5, \omega_6 \}\), ou seja, valores de 1 a 6. Neste caso o nosso evento de lançar o dado resulta em 6 estados. Sendo assim, a probabilidade é uma medida de que leva em consideração as possibilidades de um determinado estado ocorrer em um evento (perceba que essa é uma visão frequentista, ainda vamos chegar na Bayesiana). Para ser considerada uma medida \(p\) ser considerada uma probabilidade, ela tem que satisfazer as seguintes condições:

1. \(p(\Omega) = 1\), em outras palavras, \(\sum_{i} \omega_i = 1\)
2. \(p(\emptyset) = 0\), isto é, um evento impossível tem probabilidade zero
3. Sendo \(\omega_A, \omega_B \in \Omega\) então: \(p(\omega_A \cup \omega_B) + p(\omega_A \cap \omega_B) = p(\omega_A) + p(\omega_B)\)
4. Sendo \(\omega_A, \omega_B \in \Omega\) então: se \(\omega_A \subset \omega_B\) então \(p(\omega_A) \leq p(\omega_B)\)

As duas primeiras propriedades são as definições dos estados certo e impossível. A terceira é a propriedade de aditividade. Não vou entrar a fundo em teoria da medida, mas de maneira geral, a probabilidade é uma medida aditiva. Isso que dizer que a contribuição em valor dado por dois estadps é a soma dos mesmos (em medidas não aditivas pode ocorrer que a contribuição de A e B resulte em um valor maior ou menor do que soma dos dois). A quarta e última é a propriedade de ordem. Considerando nosso exemplo de rolar um dado, imagine que adicionamos o estado \(\omega_{<3}\), que é o resultado: obter um número menor que 3. O estado \(\omega_{1}\) já está contido em \(\omega_{3}\), logo sua probabilidade não pode ser maior que a deste.

Probabilidade condicional

Muita das vezes queremos calcular a probabilidade de um evento sabendo que outro evento já ocorreu. Neste caso, temos uma informação prévia. Esse tipo de probabilidade é conhecida como probabilidade condicional. Portanto, considerando \(\omega_A, \omega_B \in \Omega\), temos que a probabilidade de \(\omega_A\) dado que \(\omega_B\) já aconteceu, é definido por:

\[p(\omega_A \mid \omega_B) = \frac{p(\omega_A, \omega_B)}{p(\omega_B)} \tag{1}\]

A probabilidade \(p(\omega_A, \omega_B)\) é conhecida como probabilidade conjunta e vamos tratar dela na sequência. De maneira geral, ela é a probabilidade de ambos \(\omega_A\) e \(\omega_B\) ocorrerem. Observe que a probabilidade condicional só existe se \(p(\omega_B) > 0\). Se pensarmos bem, se \(\omega_B\) nunca ocorre, não faz sentido calcular nada condicionado a ele.

Probabilidade conjunta

As vezes temos interesse em saber a probabilidade de mais de uma estado ocorrer ao mesmo tempo. Podemos considerar 1 ou mais eventos; Por exemplo, considere que rolemos um dado e em seguida lançamos uma moeda. Qual a probabilidade de obtermos coroa e 4? Nesse caso, a probabilidade seria:

\[p(\omega_{co}, \omega_4) = p(\omega_{co})p(\omega_4) \tag{2}\]

Porém, a equação 2 só é válida pois os dois eventos são independentes, ou seja, o fato de obter cara ou coroa não interfere no valor obtido do dado. Observe que o cálculo dessa probabilidade nada mais é do que a manipulação da equação 1. Porém, \(p(\omega_{co} \mid \omega_4) = p(\omega_{co})\) uma vez que os eventos são independentes. Sendo assim, a generalização da probabilidade conjunta de dois estados é descrita a seguir:

\[p(\omega_A, \omega_B) = p(\omega_A \mid \omega_B) p(\omega_B) \tag{3}\]

A equação 3 reflete a probabilidade conjunta para dois eventos, porém, podemos generalizar para \(n\) utilizando a regra da cadeia de probabilidades condicionais:

\[p(\omega^n, \cdots, \omega^1) = \prod_{k=1}^n p(\omega^k \mid \omega^{1}, \cdots, \omega^{k-1}) \tag{4}\]

Por exemplo, para três eventos, temos:

\[p(\omega^3, \omega^2, \omega^1) = p(\omega^3 | \omega^2, \omega^1) p(\omega^2, \omega^1) \\ p(\omega^3, \omega^2, \omega^1) = p(\omega^3 | \omega^2, \omega^1) p(\omega^2 \mid \omega^1) p(\omega_1)\]

Probabilidade marginal

Imagine que temos dois eventos \(A\) e \(B\). Imagine também que sabemos as probabilidades dos estados combinados, mas queremos saber a probabilidade de um estado específico. Esta operação é conhecida como probabilidade marginal e é definida fizando o estado que queremos e variando os demais, como descrito a seguir:

\[p(\omega_a) = \sum_{\Omega_B} p(\omega_a, \omega_b) \tag{5}\]

Tentado explicar de maneira didática a equação acima, imagina o experimento de rolar o dado e lançar uma moeda. Esse experimento vai gerar um conjunto \(\Omega\) que é formado por todos os estados de ambos os eventos: \(\Omega = \{ (\omega_{co}, \omega_1), (\omega_{ca}, \omega_1), \cdots, (\omega_{ca}, \omega_6), (\omega_{co}, \omega_6) \}\). Cada um destes estados possui uma probabilidade. Agora imagina que desejamos calcular a probabilidade de se obter cara, ou seja, \(p(\omega_{ca})\). Nesse caso, somamos todas as probabilides que contém esse estado: \(p(\omega_{ca}) = p(\omega_{ca}, \omega_1) + \cdots + p(\omega_{ca}, \omega_6)\). É exatamente isso que a equação 5 faz, fixa o estado \(a\) e varia o \(b\).

Distribuições de probabilidade

Até o momento, apresentamos as definições básicas de probabilidade pensando em eventos simples, como lançar uma moeda. Acontece que a teoria da probabilidade é utilizada para modelar eventos muitos mais complexos. Vários problemas podem ser modelados ou aproximados por uma distribuição de probabilidade e é disso que vamos tratar nessa seção.

Variáveis aleatórias

Para definir uma variável aleatória, vamos considerar um experimento com um conjunto de resultados \(\Omega\). Esse experimento pode ser, novamente, lançar uma moeda, que gera um conjunto \(\Omega\) com dois resultados, \(\{\omega_{ca}, \omega_{co} \}\), ou seja, cara ou coroa. Sendo assim uma variável aleatória nada mais é do que uma variável que pode tomar um dos valores do conjunto \(\Omega\). Neste exemplo, a variável aleatória é lançar um dado e ela pode assumir os valores \(\omega_{ca}\) ou \(\omega_{co}\). Ela é aleatória pois não sabemos o seu resultado, mas podemos ter uma probabilidade dele acontecer.

Em outras palavras, uma variável aleatória é uma descrição de todos os estados possíveis de um evento. Essa variável pode ser modelada/aproximada por uma distribuição de probabilidade, que basicamente será uma função que especifica o quão provável é cada um dos estados. Além disso, variáveis aleatórias podem ser discretas ou contínuas. Em resumo, eventos discretos possuem um número finito de estados. Por outro lado, eventos contínuos são representados por números reais, portanto, assumem valores infinitos. Isso vai afetar na sua distribuição, como vamos ver na sequência.

Histogramas

Umas das melhores formas de descrever uma variável é descrevendo sua frequência no conjunto de dados. Essa descrição é conhecida como distribuição da variável. A maneira mais comum de fazer isso é por meio de um histograma, que nada mais é do que um gráfico que mostra a frequência de cada valor. A Figura 1 exemplifica esse conceito. Imagine uma turma e desejamos calcular plotar o histograma de acordo com a idade. No eixo y temos a frequência e no x as idades. Sendo assim, sabemos que temos mais alunos com 19 e 20 anos nesta turma.

Figura 1: exemplo de um histograma de idades de uma turma

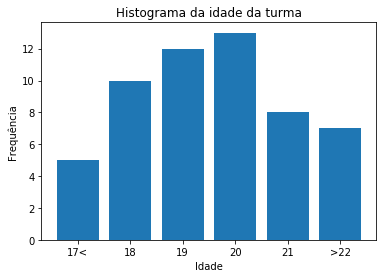
Como disse, o histograma é muito comum. Mas pode surgir a seguinte pergunta: qual a probabilidade de um aluno ter 19 anos nesta turma? Como temos as frequências, podemos simplesmente transformar esses valores em probabilidade dividindo todos pelo somatório total de todas as frequências. Dai teremos o gráfico da Figura 2.

Figura 2: exemplo de uma distribuição de probabilidade de idades

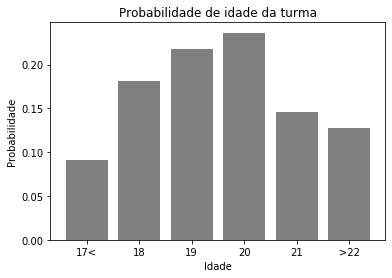
Neste caso, temos uma função de densidade de probabilidade (FDP ou PMF do inglês). Idade, nada mais é do que nossa nossa variável aleatória na qual queremos entendê-la por meio de uma distribuição de probabilidade.

Uma distribuição de probabilidade é uma descrição de quão provável uma ou mais variáveis aleatórias de tomar um determinado estado. No nosso exemplo, os estados são as idades descritas no eixo x dos gráficos anteriores. Essa distribuição é descrita por uma função que recebe como parâmetro o valor da variável e retorna a probabilidade da mesma ocorer. Porém, pode ser bem difícil encontrar essa função de maneira exata. Para facilitar nossa vida, existem diversas distribuições conhecidas que podemos aproximar para o nosso problema (vamos abordar isso nas próximas seções). Todavia, a maneira que uma distribuição é descrita depende da variável ser contínua ou discreta. O exemplo anterior é para uma função discreta, ou seja, temos um conjunto finito de idades (no caso 6) pré-definidas.

Variáveis aleatórias discretas e FDPs

Como já mostramos no exemplo anterior, para variáveis discretas, a sua distribuição de probabilidade será descrita por uma função de densidade de probabilidade (FDP). Normalmente, a notação utilizada para uma FDP é a letra maiúscula \(P\). Além disso, quando encontramos \(P(\textrm{x})\) e \(P(\textrm{y})\), normalmente, é uma distribuição para \(\textrm{x}\) e outra para \(\textrm{y}\). Essa notação é confusa, mas é a maneira que é utilizada (não me culpem).

Como já sabemos, a FDP vai mapear o estado de uma variável aleatória para uma probabilidade da variável assumir aquele estado. Sendo assim, outra fonte de confusão nas notações é que \(P(\textrm{x})\) mapeia a probabilidade de \(\textrm{x} = x\), ou seja, da variável aleatória \(\textrm{x}\) assumir um estado \(x\). Por isso, também podemos encontrar a seguinte notação \(P(\textrm{x} = x)\)

Uma distribuição pode ser com respeito a uma ou mais variáveis. No caso de duas, ela é conhecida como distribuição de probabilidade conjunta. Neste caso, teremos uma distribuição \(P(\textrm{x} = x, \textrm{y} = y)\), ou seja, a probabildiade de \(\textrm{x}\) assumir um estado \(x\) e \(\textrm{y}\) assumir um estado \(y\). A notação simplificada segue o mesmo padrão anterior \(P(x,y)\).

Para uma função ser considerada uma FDP (ok, controle a 5ª série que existe dentro de você rs) de uma variável aleatória \(\textrm{x}\), ela precisa respeitar as seguintes propriedades:

• O domínio de \(P\) deve ser o conjunto de todos possíves estados de \(\textrm{x}\).

• \(\forall x \in \textrm{x}, 0 \leq P(x) \leq 1\), além disso, um evento impossível dever ter probabilidade \(0\) e um evento garantido \(1\).

• \(\sum_{x\in \textrm{x}} P(x) = 1\). Essa é a propriedade de normalização. Nós fizemos isso no exemplo do histograma ao dividir as frequências pelo somatório total.

Exemplo de FDP

Um exemplo simples de uma FDP de uma variável aleatória \(\textrm{x}\) com \(k\) estados diferentes pode ser descrita pela seguinte equação:

\[P(\textrm{x} = x_i) = \frac{1}{k} \tag{6}\]

Essa distribuição é conhecida como distribuição uniforme. Isso significa que qualquer estado \(k\) tem a mesma probabilidade de ocorrer. O nosso exemplo de rolar um dado é descrito por essa distribuição, ou seja, obter os valores de 1 a 6 tem a mesma probabilidade. Neste caso, dizemos que a variável aleatória lançar um dado (\(A\)) segue a distribuição uniforme (\(U\)).

Por fim, é muito fácil de provar que todas as propriedades descritas acima são satisfeitas, fazendo com que essa simples função se torne uma FDP.

Variáveis aleatórias discretas e a função de distribuição acumulada (FDA)

Quando estamos trabalhando com variáveis contínuas a FDP já não é mais útil e o motivo é que mensurar a probabilidade de um único ponto contínuo pode ser complicado. Por isso é introduzida a função de distribuição acumulada (FDA). Neste caso, \(p(x)\) não será utilizado para obter a probabilidade de um ponto específico, mas sim de um intervalo. Matemáticamente falando, essa probabilidade estará em uma região inifitesimal e será calculado por uma integral.

Das regras para ser uma FDP, a única que se altera para FDA é a última. O somatório é substituído por uma integral, tomando a forma \(\int p(x)dx = 1\).

Como não estamos mais interessados em um ponto específico e sim em um intervalo, calculamos a área abaixo da curva do mesmo, ou seja, integramos a distribuição naquele intervalo:

\[p(x \in [a,b]) = \int_a^b p(x)dx \tag{7}\]

Neste curso vamos focar apenas nas distribuições discretas. No fundo, a distribuição contínua é a “generalização” da discreta. No mundo discreto uma integral nada mais é do que um somatório. Como exemplo, você pode imaginar uma distribuição uniforme para números reais. Ela pode assumir infinitos valores.

Valor esperado, variância e covariância

Valor esperado

Uma das operações mais comuns para variáveis aleatórias é o cálculo do valor esperado. Ele é uma tentativa de prever ou resumir o comportamento de uma variável aleatória. Para exemplificar sua aplicação, imagine que o tempo de entrega de uma encomenda segue uma distribuição de probabilidade \(P\). Utilizando o valor esperado é possível estimar o temo médio de entrega dessa encomenda.

A definição do valor esperado é o seguinre: Seja \(\textrm{x}\) uma variável aleatória discreta o seu valor esperado é descrito pela seguinte equação:

\[E[x] = \sum_{i=1}^n x_iP(x_i) \tag{8}\]

Observe que se a distribuição é uniforme, o valor esperado é o mesmo valor da média aritimética de um conjunto de valores.

Essa mesma definição pode ser generalizada para uma função que toma valores no espaço amostral de \(\textrm{x}\):

\[E[f(x)] = \sum_{i=1}^n f(x_i)P(x_i) \tag{9}\]

O valor esperado tem uma série de propriedades úteis e interessantes. Podemos destacar:

1. \(E\) de uma constante: \(E[\alpha] = \alpha\)
2. \(E\) de uma constante mais uma variável aleatória: \(E[\alpha + \textrm{x}] = \alpha + E[\textrm{x}]\)
3. \(E\) de uma constante vezes uma variável aleatória: \(E[\alpha \textrm{x}] = \alpha E[\textrm{x}]\)
4. O valor esperado de uma combinação linear de variáveis aleatórias: \(E[\alpha \textrm{x} + \beta \textrm{y}] = \alpha E[\textrm{x}] + \beta E[\textrm{y}]\)

Por fim, existem dois teoremas bem poderosos em relação ao valor esperado, são eles: Teorema 1: Sejam \(\textrm{x1}, \cdots, \textrm{x_n}\) variáveis aleatórias, dependentes entre si ou não, temos que:

\[E[\textrm{x1}, \cdots, \textrm{x_n}] = E[\textrm{x1}] + \cdots + E[\textrm{x_n}] \tag{10}\]

Perceba, que o teorema é basicamente uma generalização da propriedade 4, mas para mais variáveis.

Teorema 2: Sejam \(\textrm{x}_1\) e \(\textrm{x}_2\) dusa variáveis aleatórias independentes, então:

\[E[\textrm{x}_1 \textrm{x}_2] = E[\textrm{x}_1] E[\textrm{x}_2] \tag{11}\]

Variância

A variância de uma variável aleatória é uma medida que mostra o quão espalhada essa variável está. Em outras palavras, o quanto os valores que ela assume se afastam do valor esperado. Seja \(\textrm{x}\) uma variável aleatória, sua variância é descrita por:

\[Var[\textrm{x}] = E[(\textrm{x} - E[\textrm{x}])^2] \tag{12}\]

Ou, através de uma manipulação algébrica: \(Var[\textrm{x}] = E[\textrm{x}^2]- E[\textrm{x}]^2 \tag{13}\)

A variâcia é frequentemente denotada por \(\sigma^2\). O motivo é que a raiz quadrada da variância é uma medida conhecida como desvio padrão:

\[\sigma = \sqrt{Var(\textrm{x})} \tag{14}\]

A variância não segue as mesmas propriedades do valor esperado. Porém, se duas variáveis aleatórias \(\textrm{x}_1\) e \(\textrm{x}_2\) são independentes, então a variância da sua soma pode ser calculada da seguinte forma:

\[Var(\textrm{x}_1 + \textrm{x}_2) = Var(\textrm{x}_1) Var(\textrm{x}_2) \tag{15}\]

Covariância

A covariância é uma medida de quão linearmente relacionadas duas variáveis aleatórias são. Por exemplo, sejam duas variáveis aleatórias \(\textrm{x}_1\) e \(\textrm{x}_2\), o que ocorre com \(\textrm{x}_1\) se aumentarmos o valor de \(\textrm{x}_2\) ? Para isso, é utilizada a covariância, que é definida pela seguinte equação:

\[Cov(\textrm{x}_1, \textrm{x}_2) = E[(\textrm{x}_1 - E[\textrm{x}_1])(\textrm{x}_2 - E[\textrm{x}_2])] \tag{16}\]

Um valor alto positivo siginifica que ao aumetar uma variável a outra também aumenta. Por outro lado, para um valor alto negativo, se aumentarmos uma a outra diminui. Por fim, um valor igual ou próximo de zero significa que a as variáveis não apresentam uma dependência linear. Nessa parte é preciso atenção! Isso não significa que as variáveis são independentes, pois a covariância não leva em consideração relações não lineares.

Uma medida que normaliza a variância no intervalo \([-1,1]\) é a correlação. Temos, por exemplo, a correlação de Pearson, definida como:

\[\rho = \frac{Cov(\textrm{x}_1, \textrm{x}_2)}{\sigma_{\textrm{x}_1}\sigma_{\textrm{x}_2}} \tag{17}\]

Neste caso, \(+1\) indica uma correlação crescente perfeita, \(-1\) uma decrescente perfeita e \(0\) uma não correlação.

Principais distribuições de probabilidade

Existem diversas distribuições de probabilidade que são muito comuns de serem utilizadas para modelar problemas no mundo real. Nesta seção, vamos introduzir apenas 3: Bernoulli, Gaussiana e Poisson. Porém, existem diversas outras como t-student, exponencial, Beta, Dirichlet etc. Obviamente, não vamos abordar todas elas e caso você precise, recorra as referências.

Distribuição de Bernoulli

A distribuição de Bernoulli é uma das mais básicas existentes, na qual a variável aleatória pode tomar apenas dois valores, \(0\) ou \(1\). Em outras palavras, ela é binária. A distribuição é especificado por um único parâmetro \(p\) e por convenção a distribuição retorna a probabilidade da variável aleatória ser igual a \(1\), ou seja, \(P(\textrm{x}=1)\).

A equação que descreve a distribuição é apresentada a seguir:

\[P(\textrm{x}) = p^x(1-p)^{1-x} \tag{18}\]

Apenas para exemplificar podemos modelar a variável aleatória cara ou coroa utilizando Bernoulli. Neste caso, a probabilidade de se obter cara (1) ou coroa (0) pode ser equacionada por 18 quando \(p=0.5\), ou seja: \(P(\textrm{x}) = 0.5^x(0.5)^{1-x}\).

Obviamente podemos calular o valor esperado e variância da distribuição, que serão iguais a \(p\) e \(p(1-p)\), respectivamente.

Distribuição de Poisson

Outra distribuição famosa é a de Poisson, que é muito utilizada para modelar problemas que envolve uma série de eventos em um certo período de tempo. Esses eventos devem possuir uma taxa média fixa de ocorrência e ocorrem independentemente do último evento ocorrido. Sendo \(\lambda\) a taxa média de ocorrência, a distribuição e descrita da seguinte forma:

\[P(\textrm{x}) = \frac{e^{-\lambda} \lambda^x}{x!} \tag{19}\]

Nesta distribuição, tanto o valor esperado quanto a variância são iguais a \(\lambda\). Dois exemplos de problemas que podem ser modelados por Poisson são: batimentos cardíacos e chamadas telefônicas, ambas por unidades de tempo.

Distribuição Gaussiana

A distribuição Gaussina ou Normal é uma das distribuições mais utilizadas para modelar fenômenos naturais. Ela é extremamente versátil e pode ser utilizada para uma grande variedade de contextos. Obviamente, será muito utilizada em machine learning.

A Gaussiana é especificada por dois parâmetros, a média (\(\mu\)) e o desvio padrão (\(\sigma\)). Sua FDP é descrita por:

\[P(\textrm{x}) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \tag{20}\]

O gráfico dessa distribuição é ilustrado pela Figura 3:

Figura 3: variação da forma da Gaussiana de acordo com a média e desvio padrão. Fonte: [2]

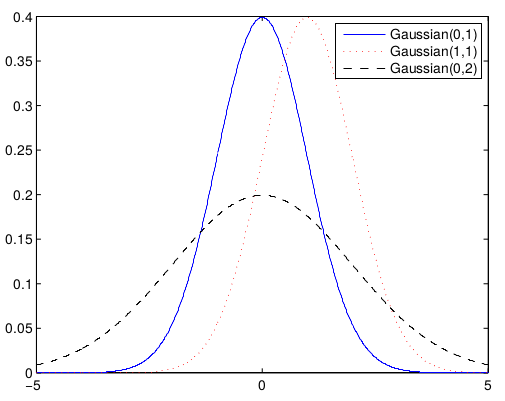
Como disse, a Gaussiana pode ser utilizada para modelar os mais diversos problemas, inclusive o nosso exemplo da seção do histograma, ou seja, modelar a idade de alunos de uma turma. Se você observar bem o gráfico da Figura 2, ele se parece um pouco com a forma de uma Gaussiana. Para plotarmos, teriamos que calcular a média de todas as idades e o desvio padrão. A partir disso é possível modelar a equação 20. Vamos brincar um pouco com essa teoria quando formos trabalhar com o classificador chamado Naive Bayes. E por falar Bayes, ele será o tema da última seção deste post.

O Teorema de Bayes

O Teorema de Bayes é um dos teoremas mais importantes da teoria da probabilidade. Em resumo, ele descreve a probabilidade de um determinado evento baseado em um conhecimento prévio sobre o mesmo. Esse conhecimento é conhecido como priore. O teorema mostra que a partir do momento que temos novas evidências alteramos a probabilidade final que é chamada de posteriori.

Para chegarmos a equação do teorema, é relativamente simples. Thomas Bayes, um matemático e pastor Inglês, observou algo interessante em relação a probabilidade conjunta. Considerando duas variáveis aleatórias \(A\) e \(B\), de acordo com a equação 3, sabemos que sua probabilidade conjunta é descrita por:

\[p(A, B) = p(A \mid B) p(B) \tag{21}\]

Porém, \(p(A, B) = p(B, A)\). Sendo assim, Bayes manipulou a equação para obter:

\[p(A \mid B) p(B) = p(B \mid A) p(A) \\ p(A \mid B) = \frac{p(B \mid A) p(A)}{p(B)} \\ \tag{22}\]

Dessa maneira, temos o famoso teorema de Bayes. Eu pretendo fazer um post dedicado só a ele. Mas de maneira geral, o que o teorema diz é: queremos estimar \(A\) dado que temos uma evidência \(B\) que influência \(A\). A \(p(A)\) é a distribuição a priori, ou seja, o que eu sei sobre uma determinada situação antes de tomar conhecimento sobre \(B\). \(p(B \mid A)\) é conhecido como likelihood. Esse é um conceito abstrato para se explicar em um resumo, mas você pode entender como o modelo de uma distribuição de acordo com alguns dados conhecidos. Já \(p(B)\) é um fator de normalização e pode ser calculado a partidar da probabilidade marginal, já discutida neste post. Por fim, \(p(A \mid B)\) é a distribuição posteriori, que queremos descobrir.

Para tentar ilustrar essa ideia com um exemplo, imagine que você esteja viajando e veja um animal que te lembra um cachorro, mas também pode ser outro animal, como um gato ou uma raposa. Mas você infere que, a probabilidade de ser um cachorro dado que estou numa estrada brasileira, é bem alta. Porém, você recebe uma nova informação que faz você mudar essa certeza que tinha que era um cachorro. Você descobre que a 50m do local onde avistou o animal existe uma ONG protetora de gatos. Com isso, automaticamente, aumenta significativamente a probabilidade do animal ser um gato, por que você teve uma nova evidência. Logo, você alterou a posteriori de acordo com a priori.

Como disse, pretendo fazer um post bem detalhado sobre estimativa Bayesiana e vou referênciá-lo aqui quando estiver pronto. Por hora, considere que o teorema existe e que ele bem importante e muito utilizado na computação em geral.

Considerações finais

A teoria da probabilidade é um dos pilares de machine learning. Você vai perceber que os algoritmos (não todos, mas boa parte) são estocásticos, ou seja, utilizam da teoria de probabilidade para gerar uma saída probabilística. Para você que achou tudo muito chato chato (neste e nos outros dois post da série), tavez você encontre mais diversão nos posts dos algoritmos. Mas saiba que a teoria é importante para você entender o que acontece por trás da chamadas dos métodos da scikit-learn.

Principais referências

[1] Deep learning - Ian Goodfellow, Yoshua Bengio e Aaron Courville link

[2] Probability Theory Review for Machine Learning - Samuel Ieong link

[3] Probability theory: The logic of science - Jaynes, Edwin T. Cambridge university press, 2003.