Operações aritméticas entre números fuzzy

Introdução

Recentemente fiz um post descrevendo os fundamentos da lógica fuzzy, caso não tenha visto, pode ser encontrado aqui. Neste post pretendo aprofundar um pouco nas operações aritméticas para números fuzzy triangulares e trapezoidais. Vamos começar definindo os números fuzzy triangulares e em seguida os trapezoidais, que possuem uma semelhança muito grande. Além disso, vamos trabalhar com números fuzzy normalizados, o que significa que existe pelo menos um valor pertencente ao \(sup_A\) tal que o seu valor de pertinência é igual a 1 (caso esteja falando grego, acesse o post sobre fundamentos da lógica fuzzy. Ao final do post, deixarei um código em MATLAB e Python de uma implementação para ambos os números os tipos de números

Tipos de números fuzzy

Como já mencionado, neste post vamos abordar dois tipos de números fuzzy, os triangulares e os trapezoidais. Exitem mais tipo, como por exemplo, o Gaussiano, mas este pode ser abordado em um post futuro.

Números fuzzy triangulares

Um número fuzzy triangular \(\tilde{a}\) é definido por \(\tilde{a} = (a_1, a_2, a_3)\) como mostrado na Figura 1.

Figura 1: exemplo de número fuzzy triangular

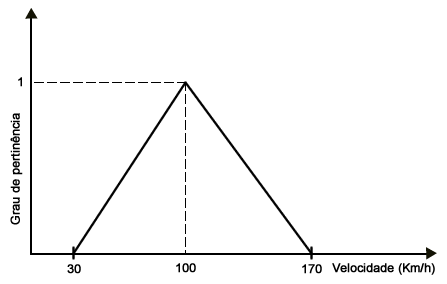
Observe que para o valor de \(x\) igual a \(a_2\) o grau de pertinência do mesmo é igual a 1, o que caracteriza o número fuzzy normalizado, e para os demais valores o grau de pertinência varia de acordo com a reta do triângulo no qual o valor pertence. Portanto, para determinar o grau de pertinência para qualquer valor de \(x\), utilizamos:

\[\mu_{\tilde{a}(x)} = \left\{\begin{matrix} 0, x < a_1 \\ \frac{x-a_1}{a_2-a_1}, a_2 \geq x \geq a_1 \\ \frac{x-a_2}{a_3-a_2}, a_3 \geq x \geq a_2 \\ 0, x > a_3 \end{matrix}\right. \tag{1}\]

Com as definições acima, podemos, então, determinar as operações aritméticas de números fuzzy triangulares como sendo:

• Soma: \(\tilde{a} + \tilde{b} = (a_1, a_2, a_3) + (b_1, b_2, b_3) = (a_1 + b_1, a_2 + b_2, a_3 + b_3)\)

• Subtração: \(\tilde{a} - \tilde{b} = (a_1, a_2, a_3) - (b_1, b_2, b_3) = (a_1 - b_1, a_2 - b_2, a_3 - b_3)\)

• Divisão: \(\tilde{a} / \tilde{b} = (a_1, a_2, a_3) / (b_1, b_2, b_3) = (a_1 / b_1, a_2 / b_2, a_3 / b_3)\)

• Multiplicação: \(\tilde{a}.\tilde{b} = (a_1, a_2, a_3) . (b_1, b_2, b_3) = (a_1 . b_1, a_2 . b_2, a_3 . b_3)\)

• Multiplicação por escalar: \(k\tilde{a} = k(a_1, a_2, a_3) = (ka_1, ka_2, ka_3)\)

Além das operações decritas acima, podemos definir também a distância entre dois números triangulares. Existem diversas formulas de distância conhecidas. Vamos definir uma usual, conhecida como distância Hamming. Sendo \(\tilde{a}\) e \(\tilde{b}\) dois números fuzzy triangulares, a distância Hamming entre os mesmos é definida como:

\[d(\tilde{a},\tilde{b}) = \frac{1}{6}[|(a_1 - b_1)| + |(a_2 - b_2)| + |(a_3 - b_3)|] \tag{2}\]

Por fim, também podemos definir uma forma de ranquear dois números fuzzy, ou seja, comparar qual é maior. Para isso, definimos a expectativa \(E\) de um número fuzzy triangular, que nada mais é que um defuzzyficação, ou seja, encontrar um número crisp que representa o número fuzzy em questão. Sendo assim, a expectativa é dada por:

\[E(\tilde{a}) = \frac{a_1 + a_2 + a_3 }{6} \tag{3}\]

Com isso, sendo \(\tilde{a}\) e \(\tilde{b}\) dois números fuzzy triangulares, \(\tilde{a} > \tilde{b}\) se \(E(\tilde{a}) > E(\tilde{b})\), caso contrário, \(\tilde{a} < \tilde{b}\). Por fim, se \(E(\tilde{a}) = E(\tilde{b})\) os dois números são iguais.

Números fuzzy trapezoildal

Um número fuzzy trapezoidal \(\tilde{a}\) é definido por \(\tilde{a} = (a_1, a_2, a_3, a_4)\) como mostra a Figura 2.

Figura 2: exemplo de número fuzzy trapezoildal

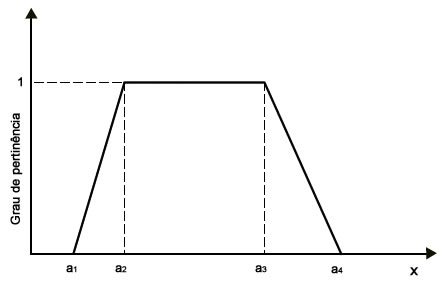
Observe que para o valor de \(x\) igual a \(a_1\) e \(a_2\) o grau de pertinência do mesmo é igual a 1.

Neste ponto você já deve ter percebido as semelhanças entre o número fuzzy triangular e o trapezoidal. Mais do que isso, já devem ter notado, que o número fuzzy triangular nada mais é do que um número fuzzy trapezoidal degenerado. Experimente fazer \(a_1 = a_2\). Sim, teremos um número fuzzy triangular! Podemos afirmar, então, que o número fuzzy trapezoidal é uma generalização dos dois modelos. A função de pertinência do número fuzzy trapezoidal é descrita por:

\[\mu_{\tilde{a}(x)} = \left\{\begin{matrix} 0, x < a_1 \\ \frac{x-a_1}{a_2-a_1}, a_2 \geq x \geq a_1 \\ 1, a_2 \geq x \geq a_3 \\ \frac{x-a_3}{a_3-a_4}, a_3 \geq x \geq a_4 \\ 0, x > a_4 \end{matrix}\right. \tag{4}\]

De forma sucinta, vamos definir, assim como no triangular, todas as operações aritméticas. Mas de maneira geral, basta acrescentar  \(a_4\) nas equações.

• Soma: \(\tilde{a} + \tilde{b} = (a_1, a_2, a_3, a_4) + (b_1, b_2, b_3, b_4) = (a_1 + b_1, a_2 + b_2, a_3 + b_3, a_4 + b_4)\)

• Subtração: \(\tilde{a} - \tilde{b} = (a_1, a_2, a_3, a_4) - (b_1, b_2, b_3, b_4) = (a_1 - b_1, a_2 - b_2, a_3 - b_3, a_4 - b_4)\)

• Divisão: \(\tilde{a} / \tilde{b} = (a_1, a_2, a_3, a_4) / (b_1, b_2, b_3, b_4) = (a_1 / b_1, a_2 / b_2, a_3 / b_3, a_4 / b_4)\)

• Multiplicação: \(\tilde{a}.\tilde{b} = (a_1, a_2, a_3, a_4) . (b_1, b_2, b_3, b_4) = (a_1 . b_1, a_2 . b_2, a_3 . b_3, a_4 . b_4)\)

• Multiplicação por escalar: \(k\tilde{a} = k(a_1, a_2, a_3, a_4) = (ka_1, ka_2, ka_3, ka_4)\)

• Distância: \(d(\tilde{a},\tilde{b}) = \frac{1}{8}[|(a_1 - b_1)| + |(a_2 - b_2)| + |(a_3 - b_3)| + |(a_4 - b_4)|]\)

• Expectativa: \(E(\tilde{a}) = \frac{a_1 + a_2 + a_3 + a_4}{8}\)

O ranking funciona da mesma maneira descrita no triangular.

Código de operações com números fuzzy

Para finalizar o post, deixo linkado uma implementação em Pyhton e MATLAB de números fuzzy triangular e trapezoidal. Essa implementação trata ambos separadamente, mas caso queira implementar a sua, nada impede de criar apenas para números fuzzy trapezoidais e quando for utilizar o triangular igualar  \(a_1 = a_2\) e utilizar as fórmulas do trapezoidal. Obviamente funciona da mesma maneira.

Link do código