Medida de desempenho de classificadores - Parte 2

Introdução

Na primeira parte deste post discutimos os conceitos básicos da medida de desempenho de classificadores. Nesta parte vamos discutir basicamente o tradeof entre precision e recall. O objetivo principal é entender como esse tradeof funciona e dissecar a curva ROC e a área abaixo da curva. Se você chegou até aqui sem ler a parte 1, minha sugestão é que clique no link acima e faça a leitura antes de continuar.

Para melhor entender esse post vamos utilizar um problema similar ao da parte 1, classificar amostras de câncer. Nesse caso, vamos considerar apenas uma amostra com Câncer ou não. Vamos manter os mesmos números do problema anterior. Para mais informações, leia a parte 1 deste post.

O tradeof entre recall e precision

Como já descrito no parte 1, nem sempre vamos conseguir um precision e um recall alto. As vezes ou muitas vezes, vamos teremos um tradeof, que nada mais é do que um troca, um compromisso. Isso significa que ao aumentar o recall, afetamos o precision e vice versa.

Para entender melhor esse tradeof vamos recorrer a Figura 1 (que foi inspirada em [1]). Nessa figura os quadrados vermelhos com a letra C representam amostras que o câncer retornou. Já os azuis com a letra O, representa as amostras em que o câncer não retornou. Portanto, neste mini exemplo temos apenas 12 amostras, que é suficiente para entender o problema. As setas azuis escuro com valores 1, 2 e 3, representam pontos de thresholds. Como já discutimos no post sobre classificação de dados, um classificador vai decidir sobre a classe de uma amostra através de um threshold, que nada mais do que um limite, um ponto de corte. Se o classificador retorna, por exemplo, uma probabilidade, podemos decidir que o threshold seja 50%, ou seja, se uma amostra tem mais de 50% de chance de não ser um câncer, a gente optar por este label. Enfim, na figura, cada seta vai representar um valor de threshold que vai afetar no resultado. Para cada seta, a direita teremos amostra classificadas como câncer e a esquerda como não câncer. Acima de cada seta estão os valores de precision, em laranja, e recall em verde. Caso não tenha entendido de primeira, sugiro que leia esse paragrafo novamente e analisando a figura com mais calma.

Figura 1: Variação do threshold de decisão entre as amostras

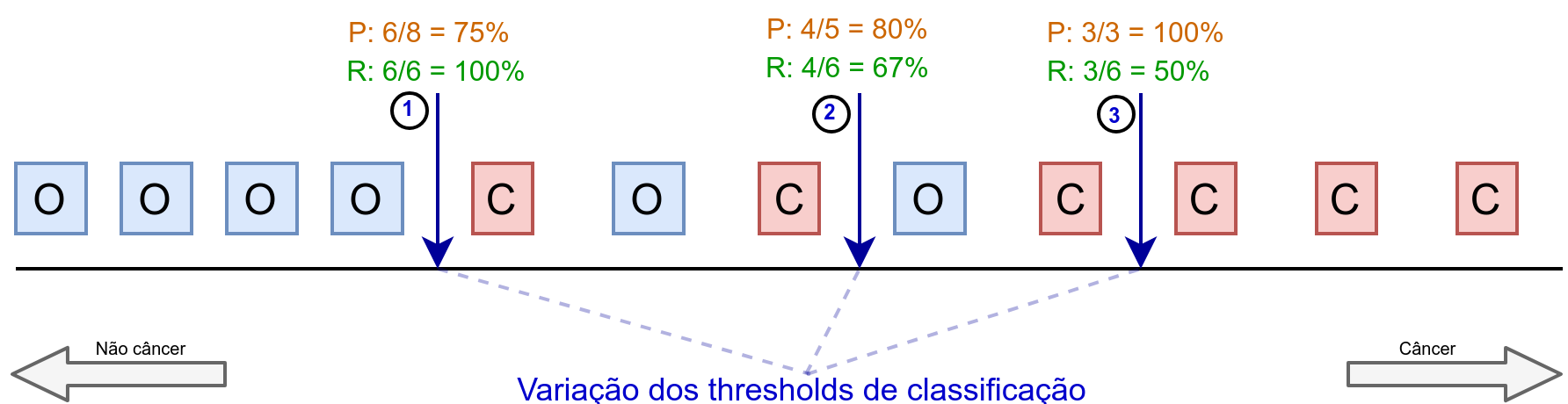
Vamos começar analisando a figura da esquerda para direita. Considerando a seta 1, podemos observar que o recall é perfeito, ou seja, das 4 amostras classificadas como não câncer, todas estão certas. Portanto, \(R = 100%\). Por outro lado, as 8 amostras classificadas como câncer, possui 2 erros. Portanto, \(P = 75%\).

Se movermos para a seta 2, ou seja, aumentarmos o valor do threshold, podemos observar aumentamos \(P\) em 5% e dinuimos \(R\) em 33%. Isso por que passamos duas amostras erradas para a equerda e deixamos apenas uma errada na direita. Por fim, se movermos mais um pouco o threshold até a seta 3, conseguimos um precision de 100% em troca de um recall de 50%. Conseguiu entender a essência do problema? Cada vez que movemos o threshold a gente ganha de um lado mas de perde de outro. Isso é um tradeof ou compromisso que devemos assumir com o problema. A pergunta natural a se fazer é: qual threshold devemos escolher? Bom, a melhor resposta é não sei, vai depender do problema (como já discutimos na parte 1). De qualquer forma, o ideal é ter em mão todas as amostras de validação classificadas para variar o threshold e escolhê-lo para o seu problema.

Plotando recall e precision x threshold

A visualização do recall e do precision de acordo com a Figura 1 é apenas ilustrativa. Para enxergamos de fato como um valor afeta no outro devemos plotar um gráficos em função do threshold. A ideia é pegar todos os valores de todas as amostras de um conjunto de treino ou validação e ir variando o threshold, consequentemente, a classificação para todas elas. O resultado é gráfico da Figura 2.

Figura 2: Precision e recall x threshold. Figura retirada de [1]

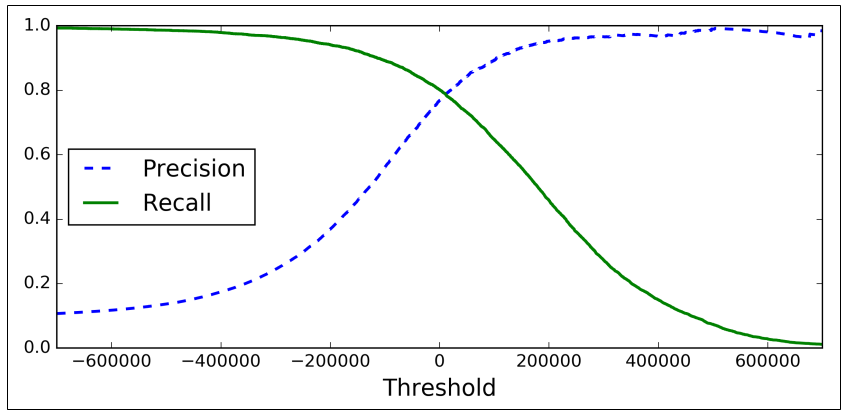
Com essa curva podemos observar que com threshold igual a zero, temos o maior valor de \(R\) e \(P\), em torno de 80%. A partir daí, se aumentarmos o threshold \(P\) aumenta, e \(R\) diminui. Por outro lado, ao diminuirmos, o contrário ocorre.

Plotando Precision x Recall

Uma outra forma de visualizar o tradeof entre as duas métricas é fazendo um plot de uma versus a outra, como mostrado na Figura 3.

Figura 3: Precision x recall. Figura retirada de [1]

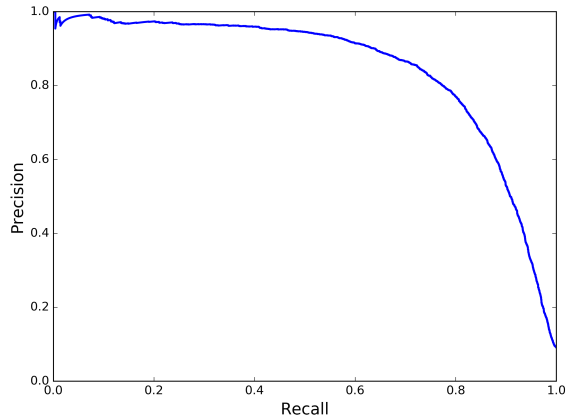
Podemos observar que para \(R \approx 0.8\), \(P\) começa a cair drasticamente. Reforçando, isso é uma escolha de projeto. Todavia, você pode escolher um valor de \(P\) de 90% é achar que esta tudo bem, certo? A má notícia é que um classificador com \(P\) muito alto não é tão útil se \(R\) for muito baixo.

A curva ROC

ROC é uma abreviação para Receiver Operating Characteristic, no fim das contas é apenas mais uma maneira de avaliar a qualidade da classificação de dados. Ela é muito similar a curva precision x recall, porém ela é baseada na curva da taxa de verdadeiro positivo (TVP) (outro nome para recall) versus a taxa de falso positivo (TFP). Como o próprio nome sugere, a TFP é a taxa de instâncias negativas que são, incorretamente, classificadas como positivas. Ela é igual a 1 menos a taxa de verdadeiro negativo(TVN), que é a taxa de instâncias negativas que são, corretamente, classificadas como positivo. Enquanto o recall ou TVP também é conhecida como sensitividade, a TVN é também conhecida como especificidade. Concluindo, a curva ROC é representada pelo seguinte plot: Sensitividade (recall) X 1-Especificidade ou TVP X TFP.

Eu sei que é muita sigla. As vezes eu também me confudo e tenho que recorrer as minhas anotações para lembra. Mas, resumindo tudo:

• Taxa de verdadeiro positivo (TVP): nada mais é do que o próprio recall. É a taxa de amostras positivas que são corretamente classificadas. Também é conhecida como sensitividade*. Definida por \(TVP = \frac{VP}{VP+FN}\)
• Taxa de verdadeiro negativo (TVN): É a taxa de amostras negativas que são corretamente classificadas. Também conhecida como especificidade. Definida por \(TVN = \frac{VN}{VN+FP}\)
• Taxa de falso positivo (TFP): É a taxa de amostras positivas que são errôneamente classificadas. Definida por \(TFP = 1 - TVN = \frac{FP}{VN + FP}\)

Plotando a curva ROC

Para plotar a curva ROC, primeiro é necessário calcular a TVP e a TFP para diferentes valores do threshold. A curva é sempre plotada com a TVP no eixo y e a TFP no eixo x. A Figura 4 exibe um exemplo de uma curva ROC.

Figura 4: A curva ROC. Figura retirada de [1]

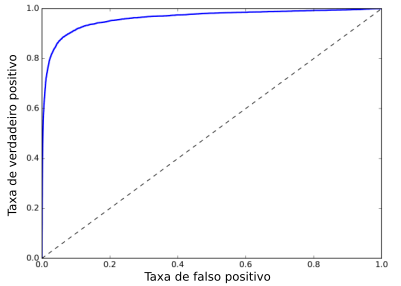
Mais uma vez, essa curva é um tradeof: quanto maior o recall, ou seja, TVP, mais falso positivos (TFP) o classificador produzirá. Em outras palavras, subir sensitividade significa baixar a especificidade e vice versa.

A linha tracejada no gráfico representa uma curva ROC de um classificador randômico. Um bom classificador ficará o mais longe possível desta linha e sempre mirando o topo esquerdo do gráfico.

Área abaixo da curva (AUC)

Uma maneira de comparar classificadores é medindo a área abaixo da curva (AUC, area under the curve). Um classificador perfeito terá AUC = 1, pois a ideia é se aproximar ao máximo do canto superior esquerdo. Quando isso ocorre, um quadrado é formado e por isso a área será 1 (vide Figura 5). Por outro lado, um classificador aleatório terá AUC = 0.5, como podemos observar na Figura 7. De maneira geral, quanto maior AUC, melhor o classificador.

Entendendo melhor a ROC

Ainda ficou com dúvida de como funciona? Ok, vamos a uma análise um pouco mais cuidadosa. Para isso, vamos recorrer a algumas figuras inspiradas em [2]. A ROC vai traçar uma curva de acordo com a distribuição das amostras do conjunto de dados. Vamos supor que sabemos as distribuições da classe positiva (amostras com câncer) (VP) e das negativas (amostras sem câncer) (VN). Um classificador com solução ideal é mostrado na Figura 5.

Figura 5: Exemplo de uma curva ROC ideal

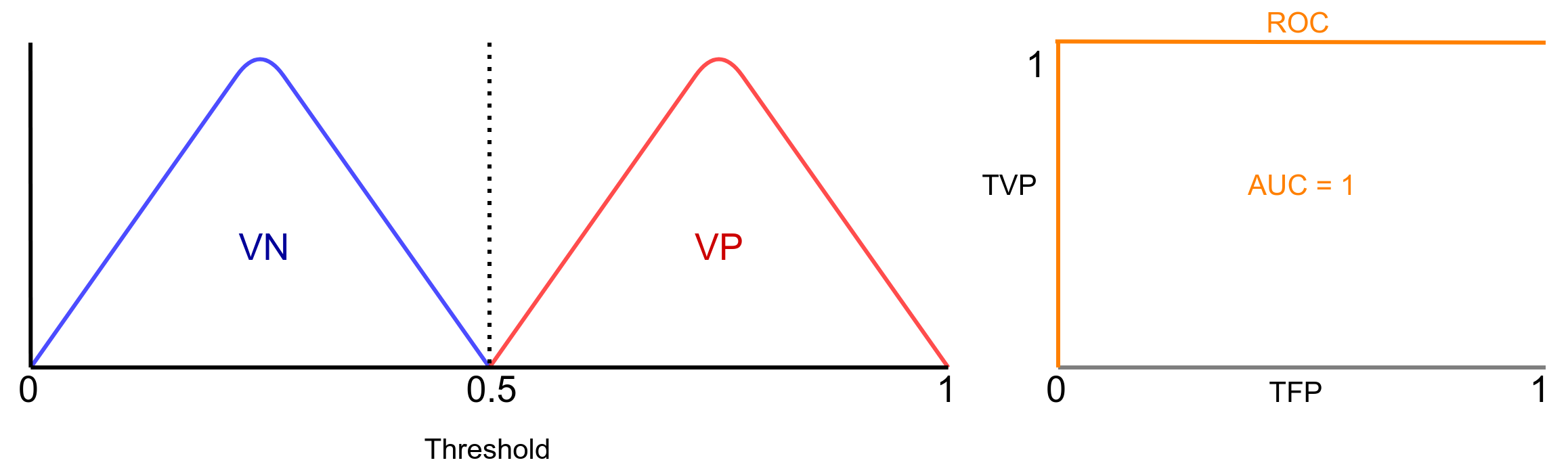
Observe que os dois conjuntos de amostras são completamente separáveis. AUC representa sempre o grau de separabilidade das classificador para com as amostras. Neste caso, AUC = 1, ou seja, completamente separável. Agora imagine a situação apresentada na Figura 6:

Figura 6: Exemplo de uma curva ROC com AUC = 0.7

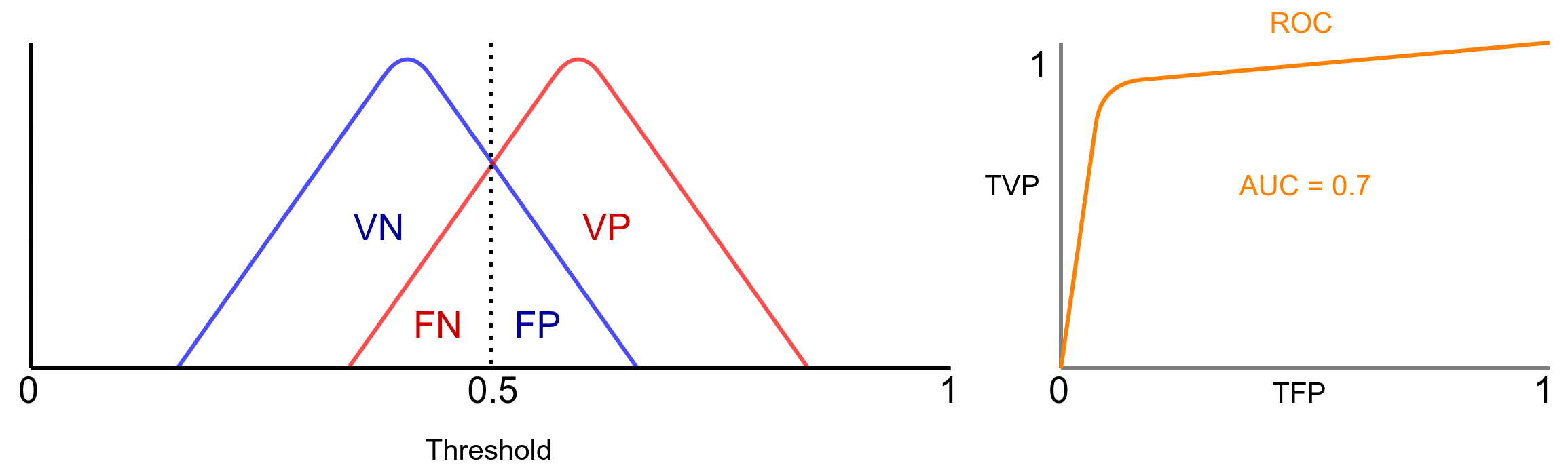
Neste caso observe que as distribuições tem sobreposições, o que faz com que surja amostras falsas positivas a negativas. Neste caso, o classificador não é mais ideal e AUC = 0.7, o que significa que o modelo tem 70% de chance de distinguir entre as amostras. Obviamente, movendo o threshold vamos priorizar uma das taxas, assim como no tradeof entre recall e precision.

O próximo caso que fictício é a sobreposição de ambas as distribuições, como mostrado na Figura 7.

Figura 7: Exemplo de uma curva ROC com AUC = 0.5

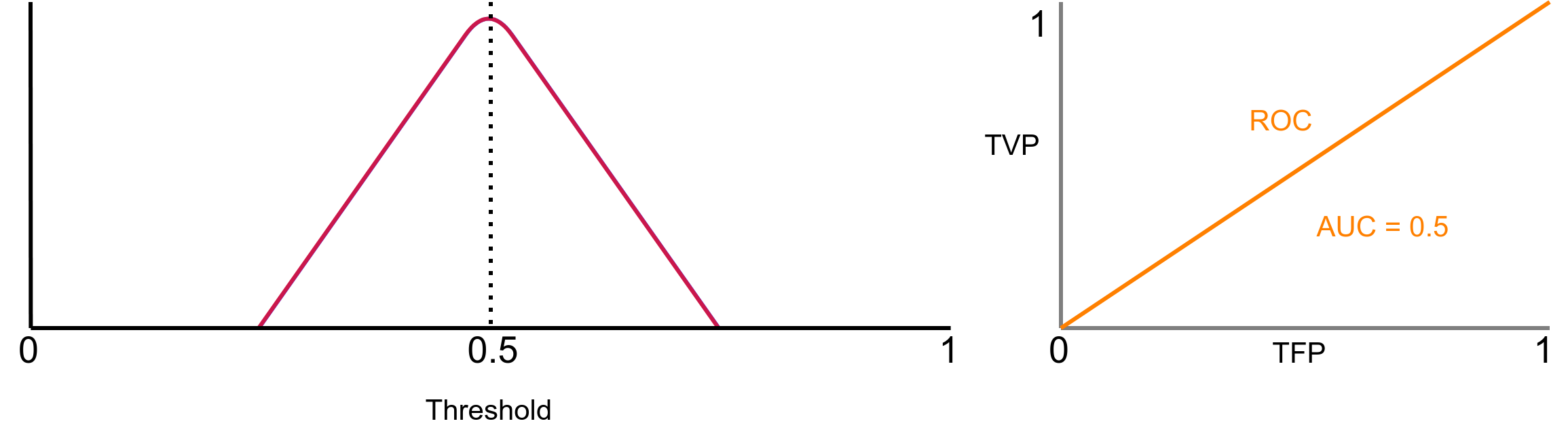
Essa é a pior situação possível. Com AUC = 0.5, nosso classificador não sabe distinguir ninguém! Ele não possui capacidade de discriminação. Esse é caso que definitivamente você não deseja. Por fim, na Figura 8 é apresentado o caso na qual AUC = 0.

Figura 8: Exemplo de uma curva ROC com AUC = 0

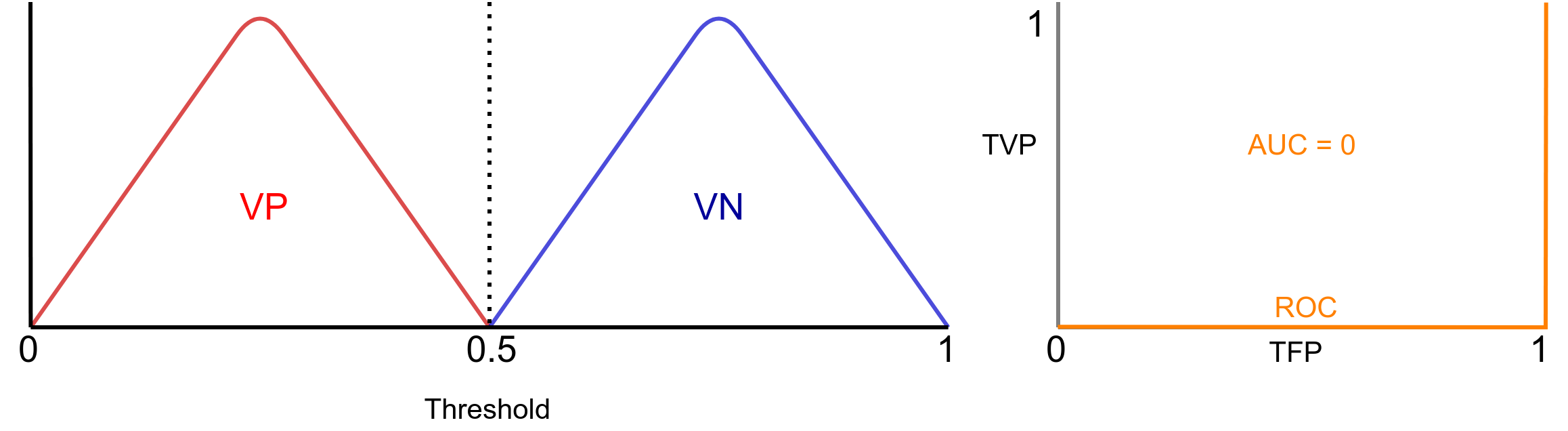
Neste caso, em um português coloquial, o classificador esta trocando as bolas. Ele classifica quem tem câncer como que não tem e vice versa. Perceba que esse não é um caso ruim, muito pelo contrário, pois apenas invertendo a saída você possui um classificador perfeito.

Como plotar ROC e calcular AUC para multiplas classes?

Assim como no parte 1, para plotar a ROC e calcular a AUC, precisamos isolar as classes e utilizar a metodologia um versus todos. Tomando como exemplo o problema com os labels A, B e C apresentado na parte 1 deste post, o princípio e basicamente o mesmo do apresentado lá. Se desejamos plotar a ROC para A, devemos considerar que B e C formam a mesma classe, no caso BC. Por isso que é um versus todos. É como se reduzissimos o problema de 3 classes para duas. Perceba que a gente fez isso na parte 1, mas não de maneira tão explícita.

Considerações finais

Nesses dois posts discutimos as medidas de avaliação de classificadores. Espero que após este longo post você tenha tirado proveito desses conceitos importantíssimos. Alias, caso queira simular/brincar com o problema, acesse este simulador de ROC. Como ele você consegue simular quase todas as situações explanadas nas figuras deste post. Você consegue mover o threshold e as distribuições e verificar como fica a curva ROC.

Então é isso! Até o próximo post!

Referências

[1] Géron, Aurélien. Hands-on machine learning with Scikit-Learn and TensorFlow: concepts, tools, and techniques to build intelligent systems. “ O’Reilly Media, Inc.”, 2017.

[2] Understanding AUC - ROC Curve - Link