Classificação de dados

Introdução

A classificação de dados está presente em diversos problemas reais, tais como: reconhecer padrões em imagens, diferenciar espécies de plantas, classificar tumores benignos e malignos, dentre outros [1]. Este problema é um dos tópicos mais ativos na área de aprendizado de máquina. Basicamente, o problema de classificação consiste em determinar o rótulo de algum objeto, baseado em um conjunto de atributos extraídos do mesmo. Para que isso ocorra é necessário um conjunto de treinamento com instâncias na qual os rótulos os objetos são conhecidos. Devido a isso, na terminologia de aprendizado de máquina, a classificação de dados é um problema de aprendizado supervisionado [2].

Definição

Formalmente, a classificação de dados pode ser definida da seguinte forma [3]:

Dado um conjunto de entradas \(X_i = \{x_1, \cdots ,x_a\}\) com \(N\) instâncias, sendo \(i=\{1,\cdots , N\}\) e \(a\) o número de atributos de \(X\), e um conjunto de rótulos de classificação \(R = \{r_1,\cdots ,r_b\}\), com \(b \ge 2\), é montado um conjunto de dados de treinamento \(T = \{(X_1,c_1),\cdots ,(X_i,c_i)\}\) no qual cada entrada \(X_i\) é vinculada a um rótulo \(c_i \in R\). O objetivo de um algoritmo de classificação é aprender, a partir de \(T\), uma correlação entre os atributos de entrada tal que: dado uma nova entrada não rotulada \(\hat{X} = \{ \hat{x_1} \cdots \hat{x_a} \}\), o classificador seja capaz de determinar o rótulo vinculado a ela.

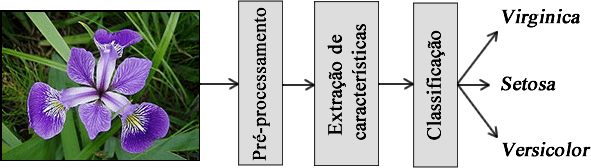
Um exemplo clássico de classificação é o problema da Iris [4]. Neste problema, existe um conjunto de flores do gênero Iris que são divididas em 3 grupos (rótulos): setosa, virginica e versicolor. Sendo assim o objetivo é determinar a qual grupo uma determinada flor pertence baseado nas medidas de sépalas e pétalas das mesmas. A Figura 1 ilustra um processo de classificação. Inicialmente as sépalas e pétalas devem ser extraídas em um pré-processamento. As medidas extraídas são processadas e suas características extraídas. Por fim, é realizada a classificação das flores. Neste exemplo os valores de \(X\) serão as medidas de comprimento e largura das sépalas e pétalas e \(R\) assumirá os rótulos setosa, virginica e versicolor.

Figura 1: Exemplo do processo de classificação de flores do gênero Iris [6]

Tipos de classificadores

A saída de um classificador pode ser apresentada de duas formas [1]:

• Rótulo discreto: neste caso, um rótulo é retornado para cada amostra.

• Valor numérico: neste caso, é retornado um valor numérico para cada rótulo. Esses valores, normalmente entre [0,1], representam o nível de aceitação da hipótese de que a amostra em questão pertença a um determinado rótulo. Normalmente, o rótulo escolhido é aquele que possui o maior valor.

A vantagem de classificadores com valores numéricos é que se torna possível comparar o grau de aceitação de cada rótulo e ranqueá-las, se for necessário. Além disso, é comum utilizar a função softmax \(\sigma(z)_k = \frac{e^{z_k}}{\sum_{j=1}^k e^{z_j} }\) em classificadores com valores numéricos, pois a mesma transforma esses valores em probabilidades [5]. Sem a softmax a saída é apenas valores numéricos. Com ela, os valores representam a probabilidade de cada rótulo para uma dada amostra. Considerando um problema com três rótulos de classificação, {A,B,C}, na fFigura 2 são ilustrados os dois tipos de classificadores já considerando o uso da função softmax no classificador de valor numérico.

Figura 2: Ilustração de um classificador abstrato e um classificador de valor numérico [6]

Por fim, é importante destacar a diferença entre problemas de classificação e de clusterização (também conhecido como agrupamento). A clusterização tem como objetivo determinar quantos grupos/rótulos de classes existem em uma determinada base de dados. Portanto, a classificação assume que as classes já são conhecidas previamente através de um processo de agrupamento. Algoritmos de clusterização utilizam similaridades entre atributos das variáveis de entrada sem conhecimento prévio de qual grupo a mesma pertence, caracterizando assim, um problema não supervisionado. Essa definição também difere dos problemas de classificação, pelo fato de aprender através de amostras com rótulos conhecidos, é considerado um problema supervisionado.

Existem diversos algoritmos para classificação de dados conhecidos. Este post teve como objetivo descrever de maneira geral, e um pouco formal,o que é um classificador. Você pode conferir nossos posts sobre alguns classificadores clássicos, como o KNN, ou classificadores que estão nos estado da arte como os que utilizam uma ELM.

Referências

[1] Aggarwal, C. C. Data classification: algorithms and applications. Minneapolis, USA: CRC Press, 2014.

[2] Kodratoff, Y. Introduction to machine learning. Palo Alto, USA: Morgan Kaufmann, 2014.

[3] Goncalves, E. C. Novel Classifier Chain Methods for Multi-label Classification Based on Genetic Algorithms. Tese (Doutorado) — Universidade Federal Fluminense, Brasil, 2015.

[4] Fisher, R. A. The use of multiple measurements in taxonomic problems. Annals of Eugenics, v. 7, n. 2, p. 179–188, 1936.

[5] Heaton, J. Artificial intelligence for humans, volume 3: deep learning and neural networks. Chesterfield, England: Heaton Research Inc, 2015.

[6] Pacheco, A. G. C. Agregação de classificadores neurais via integral de Choquet com respeito a uma medida fuzzy. Dissertação de mestrado. Universidade Federal do Espírito Santo, 2016.