Otimização por enxame de partículas - PSO

Introdução

Otimização por enxame de partículas (do inglês: Particle Swarm Optmization - PSO) é um algoritmo heurístico (assim como o Differential Evolution) baseado no comportamento social de um bando de pássaros. O método foi proposto por Eberhart e Kennedy em 1995 [1], e tem como objetivo buscar a solução ótima, em um espaço de busca, através da troca de informações entre indivíduos de uma população determinando qual trajetória cada um deles deverá tomar no espaço de busca. Caso você não tenha familiariade com problemas de otimização, sugiro o que visite o nosso post sobre o assunto.

O enxame de pássaros

No PSO, as partículas são os indivíduos da população. Fazendo uma analogia, são os pássaros de um bando. Esses pássaros exploram uma região, determinado pela função objetivo (ou fitness), a fim de encontrar a solução ótima para o problema. A posição da melhor partícula da população será a melhor posição individual, como exemplificado na Figura 1.

Figura 1: analogia de um bando de pássaros em um espaço de busca de 3D. Considerando um problema de maximização, o pássaro azul é a partícula de solução ótima do problema.

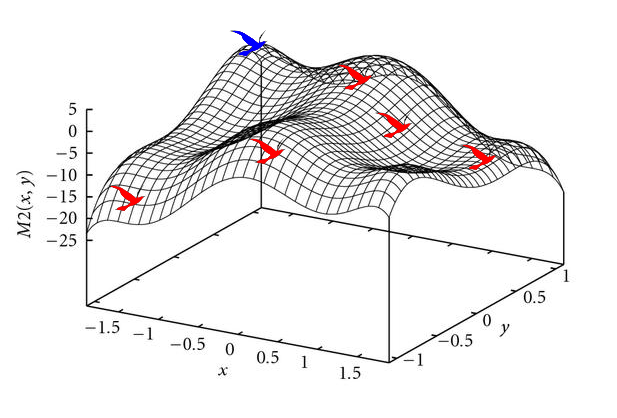
A grande vantagen de utilizar o PSO é a sua fácil implementação, usando somente estruturas primitivas e operadores matemáticos sem grande custo computacional. Obviamente, como toda heurística, o PSO não garante a solução ótima e é comum o método cair em mínimos locais. Por conta disso, existem diversas modificações no algoritmo canônico do PSO (mas nenhuma garante o ótimo, apenas aumenta a chance de sair dele). A versão apresentada a seguir é o algoritmo padrão.

Antes de iniciar o algoritmo, como já mencionado, o PSO também é baseado em população de indivíduos. Esse conceito já foi introduzido no post relacionado ao algoritmo de otimização Differential Evolution. Portanto, caso não conheça esse conceito de uma olhada no segundo parágrafo no post do algoritmo.

O algoritmo do PSO

O algoritmo do PSO é simples e são necessários poucos parâmetros para ajustes. O primeiro dele é o tamanho da população. Normalmente é utilizado uma população 10x a dimensão do problema, por exemplo, se estivermos otimizando a curva da Figura 1, uma boa escolha da população será 30, pois a função a ser otimizada possui 3 dimensões, \((x,y,z)\).

Topologias

Existem duas formas básicas de organizar a população. Essa formas são conhecidas como topologia do algoritmo e são elas: topologia global e topologia local, como mostra a Figura 2a e 2b, respectivamente. Na topologia global, todas as partículas, representadas pelas bolinhas da figura, possuem informações sobre todas as demais. Já na topologia local, uma partícula só possui informações de sua vizinha esquerda e direita. A escolha da topologia pode evitar que o algoritmo caia em mínimos locais. Por exemplo, se a função a ser otimizada é multimodal, ou seja, possui muitos máximos e/ou mínimos, uma topologia global pode convergir para um mínima/máximo local de maneira mais fácil do que a topologia local. Pode ser que agora você não tenha entendido esse conceito, mas tudo vai ficar mais claro a seguir, na qual apresentamos a equação que rege o PSO.

Figura 2: Topologias do PSO

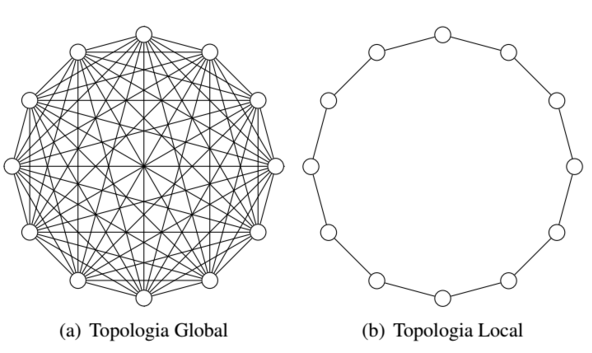
Equacionamento

Bom, sabemos que o PSO busca a solução ótima alterando as trajetórias dos indivíduos de sua população. Para fazer isso o algoritmo atualiza a velocidade e a posição de cada partícula. Considere uma população com \(K\) partículas. As variáveis \(v_k\) e \(x_k\) serão a velocidade e posição da particula \(k\), respectivamente. A velocidade e posição de cada partícula, deve ser atualizada de acordo com as equações 1 e 2, respectivamente.

\[v_{k+1} = wv_k +c_1r_1 (p_{best_k}-x_k) + c_2r_2 (g_{best} - x_k) \tag{1}\] \[x_{k+1} = x_{k} + v_{k} \tag{2}\]

As variáveis \(v_{k+1}\) e \(x_{k+1}\) serão, respectivamente, a velocidade e a posição atualizada da partícula de acordo com:

• \(w\): coeficiente de inércia
• \(p_{best_k}\): melhor posição conhecida da partícula \(k\)
• \(g_{best}\): melhor posição conhecida dentre todas as partículas
• \(c_1\) e \(c_2\): constantes de aceleração referentes ao melhor individual e global, respectivamente.
• \(r_1\) e \(r_2\): números aleatórios extraídos do intervalo [0,1]

Os valores das constantes são escolhidos de maneira empírica, de acordo com o problema em questão. Segundo [1] bons valores a serem escolhidos são: \(c_1\) e \(c_2\) iguais a 2.05 e \(w\) igual a 0.5, mas nada impede de tentar outros. As variáveis aleatórias \(r_1\) e \(r_2\), deverão ser extraídas de uma distribuição uniforme e são atualizadas a cada cálculo de velocidade da população. Obviamente as melhores posições, individuais e globais, são obtidas através da função de fitness.

Passo a passo do algoritmo

O passo a passo do algoritmo é apresentado a seguir:

1. Inicializar uma população de \(K\) indíviduos de dimensão \(D\). Essa inicialização deve ser uniforme, se o espaço de busca for conhecido. Caso contrário, inicialize aleatoriamente.
2. Determinar os valores das constantes.
3. Verificar se o critério de parada foi atingido, e esse critério pode ser um valor pré-determinado ou número de iterações. Se sim, finalizar o algoritmo.
4. Sortear os números aleatórios para \(r_1\) e \(r_2\).
5. Determinar a melhor posição global e individual.
6. Atualizar a velocidade das particulas.
7. Atualizar as posições das partículas
8. Voltar ao passo 3

Dado o algoritmos e suas duas simples equações, observamos que o PSO nada mais é do que uma atualização de velocidade e posição no espaço de busca até que uma solução suficientemente boa seja encontrada. Por fim, faço algumas observações pertinentes

• Quanto a função de fitness: obviamente você deve defini-la previamente, ela vai mudar de problema para problema. É ela que vai determinar qual é o seu espaço de busca e o quão difícil ele é. É ela que você deseja otimizar. Não entrei muito em detalhes em relação a ela pois já a discutimos nos linkados na introdução deste post.
• Quanto a topologia: voltando a discussão de topologia, agora deve ficar claro o porque ela influência no problema. Observe que a versão apresentada utiliza a topologia global, pois todas as partículas são atualizadas a partir da melhor posição global. Isso pode ser ruim, dependendo do problema. Como já disse, se a função a ser otimizada possui muitos máximos e/ou mínimos, pode acontecer de uma partícula cair em um mínimo/máximo local, e influenciar todas as outras a irem para lá. Com isso, o algoritmo terá uma convergência prematura, atrapalhando no desempenho do mesmo. A topologia local ajuda a evitar esse problema, mas a convergência pode ficar mais lenta. Como as partículas possuem a informação de melhor posição apenas de seus vizinhos, o risco delas convergirem para a mesma posição ao mesmo tempo é mínimo.

Código do PSO

Como de costume, deixo linkado o meu repositório pessoal com um código do PSO em MATLAB. Para utilizá-lo, basta alterar a função de fitness e suas constantes, caso queira. O código é aberto e você pode utilizá-lo, desde que seja dado os devidos créditos. Nos vemos no próximo post.

Referências

[1] Eberhart, R. C. and Kennedy, J. (1995). A new optimizer using particle swarm theory. In Proceedings of the sixth international symposium on micro machine and human science, volume 1, pages 39–43. New York, NY.