O algoritmo genético - GA

Introdução

O algoritmo genético (do inglês: genetic algorithm - GA) é um método evolutivo de otimização introduzido por John Holland em 1975 [1] e mais tarde foi popularizado por David Goldberg [2]. O GA se inspira nos princípios da teoria da seleção natural, proposta por Charles Darwin, na qual somente os indivíduos mais aptos sobrevivem para uma próxima geração. Como o GA é um algoritmo de otimização, é necessário entender o que é um problema de otimização. Caso não seja familiar com assunto, sugiro fortemente que acesse o nosso post o leia antes de continuar. Caso você já domine este assunto, siga em frente.

Assim como o PSO e o DE, já apresentados neste blog, o GA também utiliza uma população de indivíduos (também chamada de cromossomos). Essa população será submetida a 3 operadores: seleção, crossover (ou cruzamento) e mutação. Aplicando estes operadores de maneira iterativa, ao fim de um critério de parada pré-estabelecido, o algoritmo entrega a otimização desejada (ou algo próximo dela). Neste ponto, se você leu o post na qual discutimos sobre o DE, já deve ter percebido que ambos os algoritmos são muito semelhantes.

Teoria da seleção natural

Para entender a ideia por trás do GA, vamos fazer uma analogia com a teoria da seleção natural, de onde o algoritmo foi inspirado. Imagine uma família com pai, mãe e filho. O filho é gerado a partir da combinação dos genes de seus pais. Agora imagine milhares de pessoas se relacionando, gerando filhos (ou seja, uma população) e transmitindo seus genes (essas seriam as etapas de cruzamento e mutação do algoritmo). De acordo com Darwin, somente os indivíduos mais aptos sobrevivem para perpetuar a espécie. Isso ocorre por conta de uma seleção, que neste caso, é natural. Da população de filhos, os genes mais aptos serão transmitidos para as próximas gerações de população. Porém, a seleção natural leva muito tempo para evoluir nossa espécie (não entrarei nas discussões biológicas, filosóficas e afins). A ideia do GA é simular esse procedimento para otimizar algum problema. Um dos vídeos mais legais relacionados a seleção natural é da série quer que desenhe. Caso tenha interesse, sugiro fortemente que assista, vale muito a pena.

O algoritmo GA

Bom, dado a breve introdução, vamos ao algoritmo de fato. O GA pode ser implementado para números binários ou contínuos. A versão apresentada aqui, será a contínua, todavia vamos apenas ilustrar a ideia binária, pois a mesma é bem interessante quando comparada com o processo da evolução natural.

Tipos de populações

Na Figura 1a é apresentada uma população de \(N\) indivíduos ou cromossomos. Perceba que cada indivíduo é formado por uma cadeia de bits. Neste caso é interessante a nomenclatura cromossomos, pois cada cromossomo é formado por uma cadeia de genes, ou seja, cada gene é representado por 1 bit. Na Figura 1b é representada outra população, agora por números reais, na qual cada gene é uma dimensão. Obviamente trabalhar com a combinação de bits é mais trabalhoso do que com números reais.

Figura 1: exemplo de populações do GA

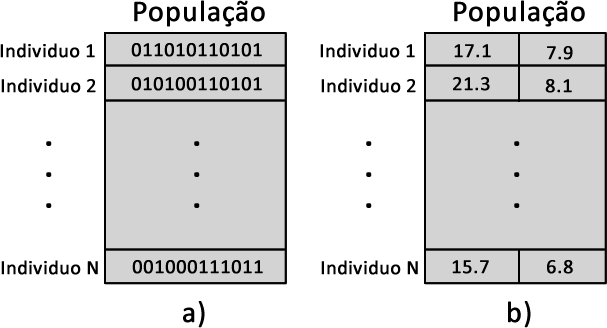
Operações do GA

Agora vamos as operações do algoritmo para valores reais. O primeiro passo a ser tomado é gerar uma população aleatória de tamanho \(N\). Chamaremos essa população de \(pop_p\) (população principal). Se o tamanho do espaço de busca for conhecido, gere os valores por meio de uma distribuição de probabilidade uniforme. Caso contrário, gere de uma distribuição normal. O tamanho da população utilizado é escolhido de maneira empírica. Normalmente se utiliza \(N\) igual a 10 vezes a dimensão do problema a ser otimizado, ou seja, se a função objetivo for \(f(x,y,z)\), estamos otimizando um problema de 3 dimensões (novamente, se você não sabe o que é uma função objetivo, acesse o nosso post sobre o problema de otimização linkado na introdução).

Seleção

Gerada a população, o primeiro operador a ser utilizado é a seleção. Nesta etapa é gerada uma população intermediária \(pop_i\), também de tamanho \(N\), a partir da \(pop_p\), da seguinte forma:

1. São sorteados dois indivíduos pertencentes a \(pop_p\) e são comparados por meio da função objetivo previamente determinada. O individuo mais apto, ou seja, com melhor valor na função objetivo segue adiante para a \(pop_i\).
2. O passo anterior é repetido até que as \(N\) posições de \(pop_i\) sejam preenchidas pelos melhores indivíduos.

Crossover

O próximo operador a ser realizado é o crossover. Nesta etapa é realizado o cruzamento entre indivíduos com intuito de gerar novos indivíduos. Se fosse na versão binária, os bits de dois indivíduos seriam cruzados. Como esta é uma versão com números reais, o cruzamento é realizado por meio de uma combinação linear de dois indivíduos da seguinte forma:

1. Primeiramente é determinada uma taxa de crossover. Essa taxa indica a probabilidade de dois indivíduos serem cruzados, portanto nem todos os indivíduos serão cruzados. Normalmente, valores em torno de 70% são boas escolhas. Essa taxa ajuda na diversidade da população. E diversidade, significa uma menor suscetibilidade a mínimos ou máximos locais.
2. Em seguida, são sorteados dois indivíduos \(pop_i\), chamaremos de \(c_1\) e \(c_2\). Por meio de uma variável aleatória, verificamos se a taxa de crossover é satisfeita, se sim é realizado a operação. O crossover apresentado aqui vai gerar dois novos indivíduos, \(p_1\) e \(p_2\), da seguinte forma:

\(p_1 = \beta c_1 + (1-\beta)c_2 \tag{1}\) \(p_2 = (1-\beta) c_1 + \beta c_2 \tag{2}\)

Sendo \(\beta\) uma constante gerada a partir de uma distribuição normal com média 1 e desvio padrão 0. Os indivíduos \(p_1\) e \(p_2\) serão alocados em uma nova população intermediária \(pop_{ii}\).

1. Caso a taxa de crossover não seja atendida, ou seja, \(c_1\) e \(c_2\) caíram nos 30% que não irão sofrer crossover, os mesmos são transmitidos diretamente para \(pop_{ii}\), isto é, \(p_1 = c_1\) e \(p_2 = c_2\).

Obviamente \(pop_{ii}\) terá o mesmo tamanho \(N\) das demais e essa etapa é repetida até que todos os indivíduos de \(pop_{ii}\) sejam determinados.

Mutação

Realizado o crossover, o próximo operador é a mutação. Este operador também auxilia na diversidade e nada mais é do que a inserção de um ruído alguns indivíduos da população \(pop_{ii}\). Na versão binária, seria nada mais nada menos do que alterar o valor de 1 ou 2 bits. Portanto, assim como no crossover, teremos uma taxa de mutação. Aqui, um valor de 10% já é suficiente. Com isso, apenas uma pequena parcela da população vai ser mutada. Sendo \(m_1\) um indivíduo pertencente ao conjunto de 10% a ser mutado, fazemos:

\(m_1 = m_1 \alpha \tag{3}\) Sendo \(\alpha\) um ruído obtido por uma distribuição normal de média 0 e desvio padrão 1.

Bom, realizado todos os operadores, neste ponto temos a \(pop_p\), que é a nossa primeira geração, a \(pop_{i}\) e a \(pop_{ii}\). Agora o algoritmo é iniciado novamente com o operador de seleção entre a \(pop_p\) e a \(pop_{ii}\). Com isso, cada iteração do algoritmo vai selecionar os indivíduos mais aptos para seguir para as próximas gerações como mostra o fluxograma da Figura 2. O algoritmo só para quando um critério de parada for alcançado. Esse critério pode ser o número de iterações, erro mínimo ou convergência da população, você escolhe de acordo com o problema que esta trabalhando.

Figura 2: Fluxograma do algoritmo GA

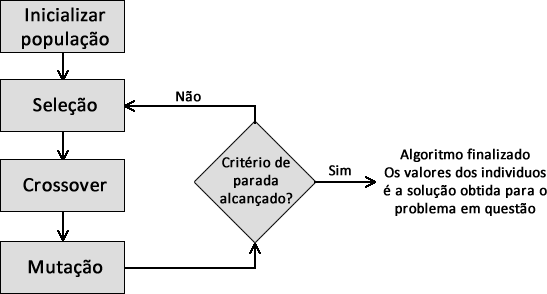
Código do algoritmo

Como de praxe, deixo uma implementação da versão discutida neste post em MATLAB. Antes de encerrar, deixo claro que existem diversas outras versões e alterações no GA e a mostrada aqui é apenas uma delas. Perceba que as constantes a ser definidas, como taxa de aprendizagem e de mutação, interferem na convergência do seu algoritmo. Esses valores podem variar de problema para problema e por conta disso existem outras abordagem para se realizar crossover e mutação. Como todo método heurístico, ele não soluciona todos os problemas e seus parâmetros afetam no desempenho final. Mas nessa altura já apresentamos 3 algoritmos evolutivos bastante utilizados atualmente, o DE, PSO e agora o GA. Você tem opção de escolher aquele que se dá melhor no seu problema. Em um próximo post podemos debater sobre uma outra heurística inspirada na natureza, a colônia de formigas. Para mais conceitos relacionados ao GA, como por exemplo o elitismo, sugiro a leitura deste capítulo de livro em português e muito bem explicado.

Referências

[1] Holland , J. H. (1975). Adaptation in Natural an d Artificial Systems. MIT Press.

[2] Goldberg, D. E. (1989). Genetic algorithms in search optimization , and machine learning. Addison-Wesley.