Mapas auto-organizáveis (SOM)

Introdução

Nest post vamos discutir um pouco sobre os mapas auto-organizáveis (em inglês: self-organized maps - SOM). O SOM foi proposto por Teuvo Kohonen [1] e pode ser considerado um tipo de rede neural artificial, mas um pouco diferente da mais tradicional, na qual já apresentamos aqui no blog. O mesmo possui um modelo de treinamento competitivo, na qual os neunônios competem entre si para ajustar seus respectivos pesos de maneira não supervisionada. De maneira geral, este algoritmo, e suas variantes, podem ser utilizadas para redução de dimensionalidade de bases de dados. Todavia, seu principal objetivo é agrupar dados semelhantes entre si, ou seja, lidar com o problema de clusterização, também já abordado neste blog.

Funcionamento de um SOM

Arquitetura

Existem diferentes aquiteturas para um SOM; porém, a mais utilizada é a bidimensional como ilustrado na Figura 1. Como pode ser observado, a rede é como um grid 2D, na qual cada entrada estará conectada a todos os neurônios do mapa, que neste caso possui 20 neurônios em um grid \(4 \times 5\). Além disso, observe que não existe conexões entre os neurônios da rede. Cada neurônio possui um conjunto de peso de dimensão igual ao número de features do conjunto de dados. Por exemplo, se nosso conjunto for a base de dados da Iris, ou seja, possui 4 features (largura e comprimento de pétalas e sépalas), cada neurônio vai possuir 4 pesos, cada um deles conectados a uma feature diferente. Portanto, sendo \(X_k = (x_1, x_2, ... , x_k)\) uma entrada, teremos uma matriz de pesos igual a \(W_{m,n} = (w_1, w_2, ..., w_k)\), sendo \(k\) a dimensão da entrada e \(m\) e \(n\) o formato do grid.

Figura 1: arquitetura 2D de um SOM

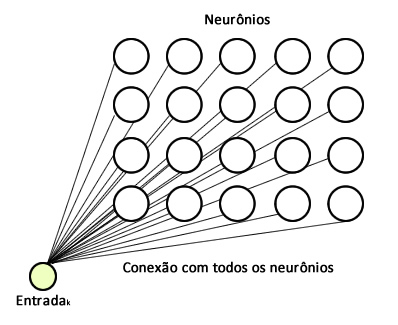
Obviamente, o número de entradas depende da base de dados utilizada e a quantidade de neurônios deve ser definida previamente. Como já mencionado, essa é a arquitetura mais utilizada, mas você pode encontrar outras de uma dimensão, três e assim por diante. Além disso, observe que o fato dos pesos não serem compatilhados faz com que a rede não seja tão eficiente quanto um convolução.

Treinamento

O treinamento de um SOM é relativamente simples. A ideia principal do algoritmo é criar grupos de neurônios especialistas em certas entradas. Essa ideia é inspirada no cérebro humano, na qual temos regiões diferentes que são responsáveis pela visão, audição, etc. Podemos dividir o treinamento em duas etapas: a competitiva e a cooperativa. Começamos sempre pela etapa competitiva.

Etapa competitiva

Para uma dada entrada \(z\), calculamos a distância dela em relação a cada um dos neurônios. O neurônio mais próximo é considerado o neurônio vencedor. Esse neurônio irá influenciar o peso de seus vizinhos para formar uma região especialista. Para calcular a distância, podemos utilizar diversas métricas. A mais comum é boa e velha distância Euclidiana:

\[d(\mathbf{x}, \mathbf{w}) = \sqrt{\sum_{i=1}^k (x_i - w_i)^2}\]

Etapa cooperativa

O intuito dessa etapa é ajustar os pesos de cada um dos neurônios da rede. Como o objetivo da rede é criar regiões especialistas, quanto mais longe um neurônio estiver de um neurônio vencedor, menos ele deve ser influenciado pelo mesmo. Além disso, com o passar do tempo, a área de influência do neurônio vencedor deve ir diminuindo. Essa ideia é ilustrada na Figura 2.

Figura 2: área de influência do neurônio vencedor diminuindo ao longo do tempo

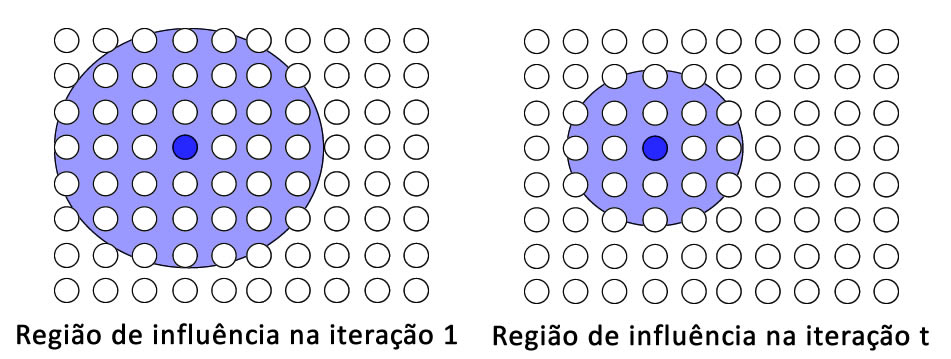
Então, resumindo até aqui: para uma entrada da base de dados, calculamos o neurônio vencedor na etapa competitiva, e agora, na etapa cooperativa, esse neurônio deve influenciar os demais. Porém, a medida que o tempo for passando, essa área de influência deve diminuir. Simples assim.

Agora temos que determinar a influência do neurônio vencedor para com os demais neurônios. Para isso, primeiro, vamos formular uma expressão de influência topológica da seguinte forma:

\[\sigma(t) = \sigma_0 e^{-\frac{t}{\tau}}\]

Na qual, \(\sigma_0 = max(m,n)\), ou seja, o valor máximo entre o número de linhas e colunas do mapa; \(t\) é uma época do algoritmo, ou seja, quando a etapa competitiva e cooperativa for executada para todas as amostras da base de dados, contamos 1 época; E por fim, \(\tau\) é uma constante de tempo definida por \(\frac{n_{\text{iter}}}{\log \sigma_0}\), na qual \(n_{\text{iter}}\) é igual o número e épocas que o algoritmo vai ser executado.

Com  \(\sigma(t)\) controlando a área de influência, definimos uma equação na qual o o neurônio vencedor (\(n_v\)) vai contribuir para alteração do peso do neurônio atual:

\[h(t) = e^{-\frac{d(n_i,n_v)}{2 \sigma(t)}}\]

Portanto, perceba que essa formulação vai calcular a distância entre um neurônio \(i\) e o neurônio vencedor e amortizar de acordo com a área de influência definida por \(\sigma(t)\). Esse princípio segue a mesma ideia de uma distribuição gaussiana/normal, ou seja, quanto mais se aproxima do centro o valor aumenta e quanto mais afasta, diminui. Aqui, vale uma observação muito importante: a distância \( d(n_i,n_v)\) é topológica, ou seja, das posições dos neurônios no grid (por exemplo, neurônio \(1 \times 1\), com neurônio \(2 \times 2\)). Cuidado para não confundir com a distância entre um neurônio e a entrada, calculadas a partir do peso.

Antes de definir a regra de atualização dos pesos dos neurônios, vamos utilizar uma taxa de aprendizagem \(\alpha(t)\). Porém, ela não será fixa, ela vai decair em relação ao tempo. Essa ideia também é inspirada no cérebro humano, no qual temos mais dificuldades de aprender de acordo com que o tempo passa. A taxa é definida da seguinte forma:

\[\alpha(t) = \alpha_0 e^{-\frac{t}{\tau}}\]

Perceba que a fórmula é bastante similar a de \(\sigma(t)\), sendo que \(\alpha_0\) é a taxa de aprendizado inicial, que deve ser informada para o algoritmo.

Atualização dos pesos

Por fim, temos que definir uma regra de atualização dos pesos da rede. Portanto, para cada neurônio do mapa, os seus respectivos pesos serão atualizados da seguinte forma:

\[W_k(t+1) = W_k(t) + \alpha(t) \times h(t) \times d(X_i, W_k)\]

Perceba que a regra de atualização dos pesos é influenciada diretamente pela distância dos mesmos para com a entrada atual \(X_i\), que por sua vez é ponderada tanto pela taxa de aprendizado quanto pelo neurônio vencedor juntamente com a posição do neurônio no grid. Ao final de um certo número de iterações ou convergência dos pesos, teremos nossa rede/mapa treinado.

Considerações finais

Bom, esse é um mapa auto-organizável! Atualmente ele não é muito utilizado, principalmente pelo custo de não ter pesos compartilhados. Mas, é sempre bom revisitar algoritmos de base para aprender mais sobre o assunto.

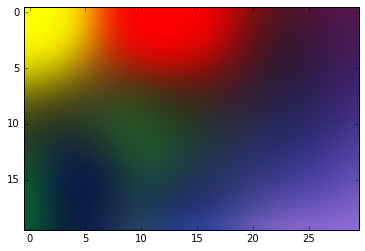
Como de costume, deixo um exemplo rápido de uma implementação do algoritmo no Github. Para acessá-lo clique aqui. Neste exemplo, a ideia é ensinar o algoritmo a clusterizar um grupo de cores. A ideia é que você obtenha um resultado como mostrado na Figura 3. Observe que as cores representam as regiões de neurônios especialistas que o algoritmo aprendeu. Dessa forma, se apresentarmos uma cor próxima do vermelho, os neurônios especialistas dessa região serão ativados.

Figura 3: resultado das regiões especialistas que o algoritmo aprendeu com cada uma das cores.

Referências

[1] Kohonen, Teuvo. Self-organized formation of topologically correct feature maps. Biological cybernetics 43.1 (1982): 59-69. p. 750–753, 1975.

[2] AI-Junkie, Kohonen’s Self Organizing Feature Maps. Disponível neste link