Introdução a Redes Neurais Artificiais

Introdução

O cérebro humano é considerado o mais fascinante processador existente. Ele é composto por aproximadamente 10 bilhões de neurônios, que são responsáveis por todas as funções e movimentos do nosso organismo. Os neurônios estão conectados uns aos outros através de sinapses, e juntos formam uma grande rede, denominada Rede Neural, que proporciona uma fabulosa capacidade de processamento e armazenamento de informação.

Há algumas décadas, surgiu a ideia de modelar, computacionalmente, as conexões neurais do cérebro humano, com intuito de emergir comportamentos inteligentes em máquinas. Neste contexto, surgiu as Redes Neurais Artificiais (RNA’s), inspiradas na própria natureza das redes de neurônios cerebrais e sinapses biológicas.

Figura 1: Rede neural humana, o melhor processador de informações existente

Redes neurais artificiais

Uma rede neural artificial é um um sistema de processamento paralelo de informações constituído pela interconexão de unidades básicas de processamento, denominadas neurônios artificiais, que tem a propensão natural para armazenar conhecimento experimental e torná-lo disponível para o uso [1]. Todo conhecimento adquirido pela rede se da através de um algoritmo de aprendizagem, cuja função é modificar os pesos de conexões entre os neurônios da rede, conhecidos como pesos sinápticos, de forma ordenada a fim de alcançar o mapeamento desejado.

O neurônio artificial

O neurônio artificial é a menor unidade de processamento de uma rede neural, que recebe sinais de entrada e produzem sinais de saída. O modelo de neurônio mais utilizado é o perceptron, representado na Figura 2. Ele é composto por: \(m\) entradas \([x_1, ..., x_m]\), \(m\) pesos sinápticos \([w_1, ..., w_m]\), uma variável de deslocamento linear \(b\) (do inglês: bias) e uma saída \(y\), que é descrita por:

\[y = f(\sum_{i=1}^m x_iw_i + b) \tag{1}\]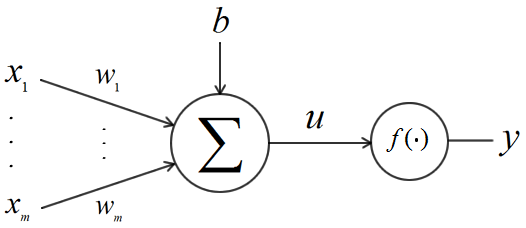

Figura 2: O modelo do neurônio artificial perceptron

A função \(f()\) é conhecida como função de ativação ou função de transferência. Ela é utilizada para adicionar uma não linearidade no sistema. Dentre as funções de ativação mais utilizadas estão a sigmóide e a relu, definidas pelas equações abaixo, respectivamente:

\[f(u) = \frac{1}{1+e^{-u}} \\ f(u) = x^{+} = max(0,u) \tag{2}\]

Arquitetura de uma RNA

A arquitetura de uma rede neural artificial está relacionada com a maneira pela qual os neurônios da mesma estão organizados. Para isso, a rede é dividida em três tipos de camadas: a de entrada, a escondida e a de saída. As camadas de entrada e saída são intuitivas e representam o número de entradas e saídas do problema em questão. Já a escondida é a camada que fará a maior parte do processo de aprendizagem da rede. Normalmente uma rede neural possui uma camada de entrada, uma camada de saída e \(k\) camadas escondidas, na qual \(k\) é definido empiricamente e varia de acordo com o problema. Com isso forma-se uma rede de múltiplas camadas.

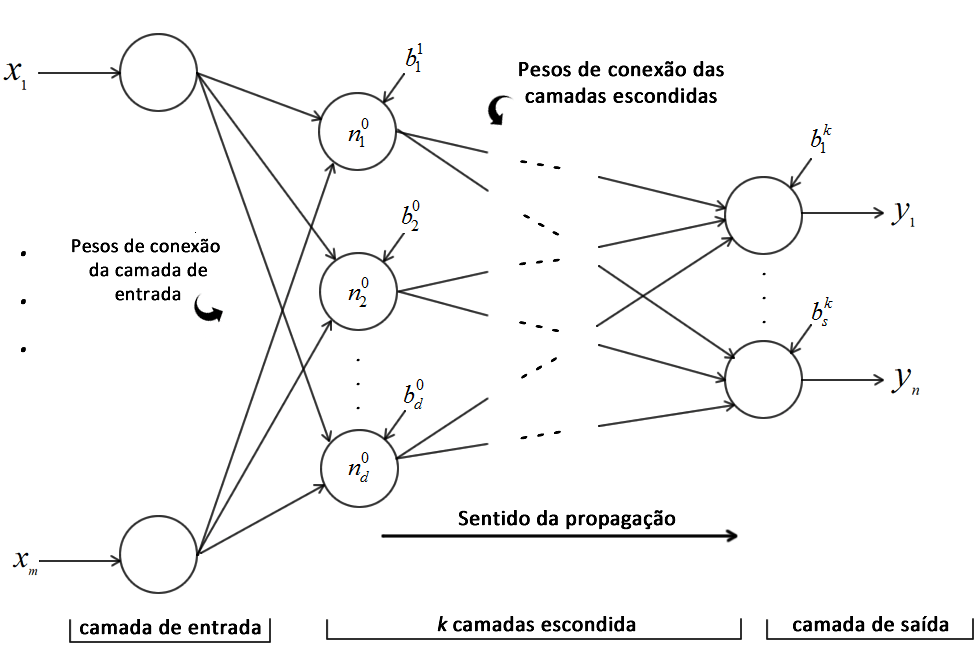
Redes neurais do tipo Feedforward (em português costumam traduzir como alimentação direta ou avante) são redes de múltiplas camadas na qual a informação só propaga em um sentido. No caso, os sinais provenientes dos neurônios de uma camada só podem estimular os neurônios da camada seguinte, não existindo realimentação. A Figura 3 mostra uma rede neural artificial de múltiplas camadas do tipo Feedforward, com uma camada de entrada, com $m$ entradas, $k$ camadas escondidas e uma camada de saída com $n$ saídas.

Figura 3: Exemplo de rede neural artificial do tipo feedforward com k camadas escondidas

Algoritmo de treinamento

Após projetada a arquitetura da rede (determinar número de entradas, saídas, camadas escondidas e número de neurônios), é necessário um algoritmo de treinamento para realizar a aprendizagem da mesma. No processo de treinamento a rede ‘aprende’ através de exemplos que relacionam as entradas e saídas do problema a ser solucionado. Essa abordagem é conhecida como aprendizado supervisionado. Dentre os algoritmos conhecidos, para solucionar esse tipo de problema, o mais utilizado é o backpropagation [2]. A ideia do algoritmo é estimar os valores dos pesos e bias minimizando uma função de custo, que nada mais é do quanto a predição da rede está errando em relação a saída original do problema. Existem diversas funções de custos, variando de acordo com o problema. Uma função de custo muito conhecida é o erro quadrático médio (MSE - do inglês, mean square error), que descrito na equação 3.

\[MSE = \frac{1}{2} \sum_{i=1}^p \sum_{j=1}^n (d_j^i - y_j ^i)^2 \tag{3}\]

Sendo \(p\) o número exemplos a ser utilizados no treinamento, \(n\) o número de saídas da rede e, finalmente, \(d\) e \(y\) as saídas desejadas e obtidas, respectivamente, para a entrada em questão.

A partir do erro calculado pela função de perda, o backpropagation utilizar uma regra de atualização para cada peso sináptico da rede, que é calculado pela seguinte equação:

\[W = W + \Delta W \rightarrow \Delta W = -\alpha \frac{\partial E}{\partial W} \tag{3}\]

na qual, \(\alpha\) é conhecido como taxa de aprendizado, que, resumidamente, indica o ‘tamanho do passo’ do gradiente rumo a minimização. O sinal negativo indica a busca por uma alteração no peso que reduza \(E\).

Não vou aprofundar muito sobre o backpropagation neste post pois tenho a inteção de escrever outro post especificamente sobre ele. Como ele é massivamente utilizado e muito importante para área de aprendizado de máquina, creio que vale muito a pena aprofundar neste assunto. Porém, vale a pena salientar, que podemos, por exemplo, treinar uma rede neural utilizando um dos algoritmos evolutivos que já apresentamos aqui neste blog. Também vamos fazer um post sobre esse assunto.

Utilizando uma RNA

Implementar um RNA do zero não é uma tarefa tão complicada, mas sugiro que utilize uma linguagem que forneça ferramenta para manipulação de matrizes. Alias, na minha visão, implementar um algoritmo é primordial para uma melhor compreensão do mesmo (eu mesmo já implementei minha RNA lá nos primordios rs). Todavia, se o intuito é obter resultados mais rápido com uma ferramenta já validada, sugiro a utilização de bibliotecas/toolboxes como a do MATLAB para RNA, que é um ambiente todo preparado para prototipação com redes neurais artificiais. Além dessa opção, outra opção que eu utilizo bastante é o Scikit-Learning, uma excelente biblioteca para Python. Em breve, vou postar um tuturial de rede neural com a biblioteca. Por hora, deixo linkado um tutorial que escrevi sobre o uso que mostra o básico de como utilizar a redes neurais no MATLAB.

Além disso, deixo um código de uma predição de uma série temporal utilizando a toolbox. A série representa a demanda mensal de energia na Austrália, entre determinado período de tempo, e a rede neural é utilizado como preditor da mesma. É utilizado 70% da série para treinar a rede e 30% para executar e checar se o resultado que a rede obteve é compatível com a realidade. Com o código sugiro que varie o número de neurônios, camadas e função de ativação para observar a influência de cada um deles no resultado final. Do mais, sinta-se livre para utilizá-lo e se encontrar algum bug, nos avise!

Referências

[1] Haykin, S., Neural Networks: A Comprehensive Foundation, Prentice Hall, 2º edition, 1998

[2] Rumelhart, D. E., Hinton, G. E. e Willians, R. J. Learning representations by backpropagating errors, Nature, v. 323, p. 533-536, 1986.