TOPSIS - Um algoritmo de tomada de decisão

Introdução

Ao longo de nossas vidas somos obrigados a tomar uma série de decisões, algumas fáceis e outras extremamente difíceis. Seja fácil ou difícil, para se fazer uma escolha, normalmente, temos alternativas a serem escolhidas de acordo com um conjunto de critérios pré definidos. Um exemplo simples pode ser escolher um carro para comprar. A maioria das pessoas leva em consideração o preço, potência do motor, reputação da montadora, conforto, etc. Esses, nada mais são que nossos critérios para escolher um carro e baseado neles, avaliamos nossas alternativas, que poderiam ser um HB20, um Pálio ou um Corola, dependendo, é claro, de quais os critérios são os mais importantes para cada pessoa. Agora imagine uma decisão mais complexa de ser tomada, como por exemplo, onde investir uma certa quantidade de dinheiro. Já imaginou um algoritmo que possa te auxiliar nessa decisão?

O algoritmo TOPSIS (em inglês, Technique for Order Preference by Similarity to Ideal Solution) foi desenvolvido por Hwang e Yoon [3] e é uma técnica de avaliação de performances de alternativas através da similaridade da mesma com uma solução ideal. De acordo com essa técnica a melhor alternativa é aquela mais próxima da solução ideal e mais distante da solução não ideal. O TOPSIS é muito utilizado para solucionar problemas de tomada de decisão da vida real, como nosso exemplo da escolha do carro. Além disso, existem variações do algoritmo que utilizam lógica fuzzy [4] e lógica fuzzy intuicionista [4], mas isso são assuntos para um próximo post.

Tomada de decisão de multi-critério

Problemas de tomada de decisão multi-critério (do inglês, multi-criteria decision making - MCDM) são caracterizados por uma matriz de decisão, que é composta de alternativas e critérios ponderados de acordo com o tomador de decisão em questão. Métodos para solucionar problemas MCDM como têm sido amplamente utilizados para selecionar a melhor alternativa entre um número finito de alternativas. Como exemplo de métodos, podemos citar PROMETHEE [1], TODIM [2] e o TOPSIS [3], que será o tema deste post.

Vamos considerar uma matriz \(D\), no qual consiste de alternativas e critérios, descrita por:

\[D = \begin{pmatrix} x_{11} & \cdots & x_{1n}\\ \vdots & \ddots & \vdots \\ x_{m1}& \cdots & x_{mn} \end{pmatrix} \tag{1}\]

Na qual, as linhas da matriz \(D\) serão alternativas, que chamaremos de \(A_{1}, A_{2} \cdots A_{m}\). Por outro lado, as colunas são critérios, que chamaremos de \(C_{1}, C_{2} \cdots C_{n}\). O valor \(x_{ij}\) indica o rating, o desempenho, da alternativa \(A_{i}\) com respeito ao critério \(C_{j}\). Cada critério possui um determinado peso, definido pelo tomador de decisão em questão (pode ser eu, você, um amigo…), representado por \(W = (w_{1}, w_2, \cdots , w_n)\), sendo \(w_j\) um peso para o critério \(C_j\) satisfazendo \(\sum_{j=1}^n w_j = 1\). Obviamente, \(i = \{1, \cdots, m\}\) e \(j = \{1, \cdots, n\}\).

Em geral os critérios são classificados em dois tipos (e isso é muito importante). Critérios de custo, quanto, menor o rating dele melhor, e critérios de benefício, quanto maior o rating melhor. Voltando ao nosso exemplo da compra do carro, o preço é um critério de custo, ou seja, quanto menor o preço, mais desejável é o carro. Por outro lado, o conforto é um critério de benefício, ou seja, quanto maior, melhor.

A matriz \(D\), depois de preenchida, necessita ser normalizada em uma matriz \(R = [r_{ij}]_{m \times n}\), isso permite a comparação entre todos os critérios (imagine, o preço dos carros estão em um intervalo bem maior do que uma nota de 0 a 10 dada para o conforto, por exemplo).

Para normalizar basta fazer:

\[r_{ij} = \frac{x_{ij}}{\sqrt{\sum_{i=1}^m x^2_{ij}}} \tag{2}\]

Por fim, após a normalização dos ratings, os valores da matriz \(R\) devem ser ponderados pelo vetor \(W\), gerando uma nova matriz \(P = [p_{ij}]_{m \times n}\), oriunda da seguinte multiplicação:

\[p_{ij} = w_j \times r_{ij} \tag{3}\]

O algoritmo TOPSIS

A seguir serão definidos o passo a passo do algoritmo de tomada de decisão TOPSIS.

Passo 1

Identificar a solução ideal positiva \(A^+\), para critérios de benefício, e a solução ideal negativa \(A^-\), para critérios de custo, como descrito a seguir:

\[A^{+} = (p^{+}_{1}, p^{+}_{2}, \cdots , p^{+}_{n}) \\ A^{-} = (p^{-}_{1}, p^{-}_{2}, \cdots , p^{-}_{n}) \tag{4}\]

Sendo:

\[p_{j}^+ = \left\{\begin{matrix} max_i (p_{ij}), \textrm{se o criterio é de beneficio} \\ min_i (p_{ij}), \textrm{se o criterio é de custo} \end{matrix}\right. \\ p_{j}^- = \left\{\begin{matrix} min_i (p_{ij}), \textrm{se o criterio é de beneficio} \\ max_i (p_{ij}), \textrm{se o criterio é de custo} \end{matrix}\right. \tag{5}\]

Em outras palavras, as equações acima escolhem os melhores desempenhos em cada critério, seja ele de custo (e nesse caso o melhor desempenho é o menor valor) ou de benefício (no qual o melhor desempenho é o maior valor), e monta os vetores \(A^+\) e \(A^-\), que nada mais são do que os desempenhos para uma alternativa perfeita, ou seja, ter ratings altos para os critérios de benefícios e baixo para os de custo.

Uma outra maneira de obter os vetores ideais, é ao invés de escolher os valores máximos ou mínimos da matriz \(P\), simplesmente é atribuído 1 ou 0 para criar a alternativa perfeita. Neste caso, no vetor ideal positivo \(A^+\), os critérios de benefícios recebem valor 1 e de custo 0. Já no vetor ideal negativo \(A^-\), a lógica inverte. Os critérios de benefícios recebem 0 e os de custo 1. Como alertei anteriormente, o conceito de custo e benefício é essencial para o TOPSIS funcionar corretamente.

Passo 2

Calcular, para cada alternativa \(A_i\) a distância euclidiana de cada rating para o vetor de soluções positivas \(A^+\) e para o vetor de soluções ideias negativo \(A^-\).

\[d_{i}^{+} = \sqrt{\sum_{j=1}^{n} (d_{ij}^{+})^2} \\ \\ d_{i}^{-} = \sqrt{\sum_{j=1}^{n} (d_{ij}^{-})^2} \tag{6}\]

Na qual, \(d_{i}^{+} = p_{j}^{+} - p_{ij}\) e \(d_{i}^{-} = p_{j}^{-} - p_{ij}\).

Passo 3

Calculado as distâncias do passo anterior, o próximo passo é determinar a proximidade relativa \(\xi\). A ideia é escolher como melhor alternativa aquela mais próxima da solução ideal positiva e mais distante da solução ideal negativa. Para isso, fazemos:

\[\xi_i = \frac{d_{i}^{-}}{d_{i}^{+} + d_{i}^{-}} \tag{7}\]

Passo 4

O último passo é fazer o ranking das alternativas baseada nos vetor \(\xi\). As melhores alternativas são aquelas com os maiores valores de \(\xi_i\) e devem ser escolhidas pois estão mais próximas da ideal.

Código exemplo

Ao final deste post deixo linkado um código em MATLAB de um exemplo fictício baseado no nosso exemplo dos carros. Suponhamos que temos as 3 alternativas listadas na introdução: Pálio, HB20 e o Corola. Eles serão avaliados em 4 critérios: consumo (C), conforto (B), preço (C) e reputação da marca (B). Os pesos, que eu definir e cada tomador de decisão defini o seus próprios pesos, de cada critério, ou seja, o quão importante o critério é para mim, serão: consumo 30%, conforto 5%, preço 60% e reputação da marca 5%. A avaliação de cada carro, segundo os critérios é mostrado na matriz abaixo (cada alternativa e critério estão na mesma sequência). O consumo esta em litros a cada 100km, o conforto de 0 a 10, o preço em reais e a reputação de 0 a 10. Obviamente os valores são fictícios!

\[D = \begin{pmatrix} 15 & 6 & 25000 & 7\\ 12 & 7 & 35000 & 7 \\ 10 & 9 & 55000 & 8 \end{pmatrix} \tag{8}\]

Nessa matriz é executado o TOPSIS (perceba que é importante a normalização, pois os valores estão em intervalos bem diferentes) e o resultado do raking final é mostrado na figura abaixo.

Figura 1: Ranking com o resultado do TOPSIS para o problema em questão

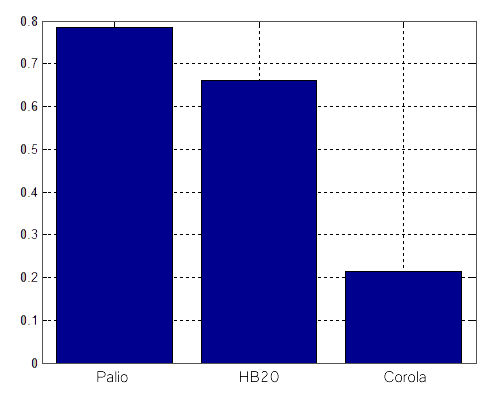
Os valores na lateral são os obtidos por \(\xi_i\). Observe, que segundo os ratings e seus respectivos pesos, que eu atribuí, o melhor carro para mim é um Pálio (e realmente eu tenho um pálio rs). Se os valores dos pesos forem alterados o ranking pode sofrer alterações. Experimente fazer isso!

Para acessar o código deste exemplo, clique aqui. Além disso, deixo linkado um código em Python para o TOPSIS. Neste mesmo repositório, existe o código para outro algoritmo de tomada de decisão, o TODIM, que certamente será tópico de outro post no futuro.

Por hoje é só pessoal!

Referências

[1] R.E. Bellman, L.A. Zadeh, Decision-making in a fuzzy environment, Management Science 17 (1970) 141-164.

[2] C.L. Hwang; K.P. Yoon, Multiple Attributes Decision Making Methods and Applications, Springer-Verlag, Berlin, 1981.

[3] L.F.A.M. Gomes, L.A.D. Rangel, An application of the TODIM method to the multicriteria rental evaluation of residential properties, European Journal of Operational Research 193 (2009) 204-211.

[4] Krohling, Renato A., and Vinicius C. Campanharo. “Fuzzy TOPSIS for group decision making: A case study for accidents with oil spill in the sea.” Expert Systems with Applications 38.4 (2011): 4190-4197.

[5] Krohling, Renato A., André GC Pacheco, and André LT Siviero. “IF-TODIM: An intuitionistic fuzzy TODIM to multi-criteria decision making.” Knowledge-Based Systems 53 (2013): 142-146.